Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Onneweer, C. W.
and
Quek, T. S.
1993.
Multipliers for Hardy spaces on locally compact Vilenkin groups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 55,
Issue. 3,
p.
287.
Kitada, Toshiyuki
1993.
Multipliers for weighted Hardy spaces on locally compact Vilenkin groups.
Bulletin of the Australian Mathematical Society,
Vol. 48,
Issue. 3,
p.
441.
Zheng, Shijun
2000.
Cesàro Summability of Hardy Spaces on the Ring of Integers in a Local Field.
Journal of Mathematical Analysis and Applications,
Vol. 249,
Issue. 2,
p.
626.
Fan, Dashan
and
Yang, Dachun
2000.
Herz-type Hardy spaces on Vilenkin groups and their applications.
Science in China Series A: Mathematics,
Vol. 43,
Issue. 5,
p.
481.
Quek, Tong Seng
and
Yang, Dachun
2001.
Calderón - Zygmund Operators on Weighted Weak Hardy Spaces in Locally Compact Vilenkin Groups.
Mathematische Nachrichten,
Vol. 225,
Issue. 1,
p.
123.
Zhu, Yueping
2002.
Multipliers on weighted function spaces over locally compact vilenkin groups.
Bulletin of the Australian Mathematical Society,
Vol. 65,
Issue. 2,
p.
337.
Yueping, Zhu
2002.
Multipliers on weighted function spaces over locally compact Vilenkin groups.
Approximation Theory and its Applications,
Vol. 18,
Issue. 2,
p.
65.
Avdispahić, M.
and
Memić, N.
2010.
Fourier multiplier theorem for atomic Hardy spaces on unbounded Vilenkin groups.
Journal of Mathematical Analysis and Applications,
Vol. 363,
Issue. 2,
p.
588.
Ho, Kwok-Pun
2021.
Calderón-Zygmund Operators on Morrey and Hardy-Morrey Spaces in Locally Compact Vilenkin Groups.
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 13,
Issue. 3,
p.
204.


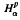 to itself or the corresponding power-weighted Lebesgue space
to itself or the corresponding power-weighted Lebesgue space