Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Heydari, Mohammad Taghi
and
Ranjbar, Sajad
2016.
Halpern-type proximal point algorithm in complete CAT(0) metric spaces.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 24,
Issue. 3,
p.
141.
Ranjbar, Sajad
and
Khatibzadeh, Hadi
2017.
Strong and $$\Delta $$ Δ -Convergence to a Zero of a Monotone Operator in CAT(0) Spaces.
Mediterranean Journal of Mathematics,
Vol. 14,
Issue. 2,
Heydari, Mohammad Taghi
Khadem, Amene
and
Ranjbar, Sajad
2017.
Approximating a common zero of finite family of monotone operators in Hadamard spaces.
Optimization,
Vol. 66,
Issue. 12,
p.
2233.
Khatibzadeh, Hadi
Mohebbi, Vahid
and
Ranjbar, Sajad
2017.
New results on the proximal point algorithm in non-positive curvature metric spaces.
Optimization,
Vol. 66,
Issue. 7,
p.
1191.
Aremu, Kazeem O.
Izuchukwu, Chinedu
Ugwunnadi, Godwin C.
and
Mewomo, Oluwatosin T.
2018.
On the proximal point algorithm and demimetric mappings in CAT(0) spaces.
Demonstratio Mathematica,
Vol. 51,
Issue. 1,
p.
277.
Chang, Shih-sen
Yao, Jen-Chih
Wen, Ching-Feng
and
Wang, Lin
2018.
A modified viscosity implicit-type proximal point algorithm for monotone inclusions and asymptotically nonexpansive mappings in Hadamard spaces.
Journal of Inequalities and Applications,
Vol. 2018,
Issue. 1,
Okeke, C. C.
and
Izuchukwu, C.
2019.
A strong convergence theorem for monotone inclusion and minimization problems in complete CAT(0) spaces.
Optimization Methods and Software,
Vol. 34,
Issue. 6,
p.
1168.
Abbas, Mujahid
Ibrahim, Yusuf
Khan, Abdul Rahim
and
De la Sen, Manuel
2019.
Split Variational Inclusion Problem and Fixed Point Problem for a Class of Multivalued Mappings in CAT(0) Spaces.
Mathematics,
Vol. 7,
Issue. 8,
p.
749.
Ugwunnadi, G. C.
Izuchukwu, C.
and
Mewomo, O. T.
2019.
Strong convergence theorem for monotone inclusion problem in CAT(0) spaces.
Afrika Matematika,
Vol. 30,
Issue. 1-2,
p.
151.
Eskandani, G. Zamani
and
Raeisi, M.
2019.
On the zero point problem of monotone operators in Hadamard spaces.
Numerical Algorithms,
Vol. 80,
Issue. 4,
p.
1155.
Izuchukwu, C.
Aremu, K. O.
Mebawondu, A. A.
and
Mewomo, O. T.
2019.
A viscosity iterative technique for equilibrium and fixed point problems in a Hadamard space.
Applied General Topology,
Vol. 20,
Issue. 1,
p.
193.
Izuchukwu, C.
Mebawondu, A. A.
Aremu, K. O.
Abass, H. A.
and
Mewomo, O. T.
2020.
Viscosity iterative techniques for approximating a common zero of monotone operators in an Hadamard space.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 69,
Issue. 2,
p.
475.
Ugwunnadi, Godwin Chidi
2020.
On the strong convergence of a modified Halpern algorithm in a CAT(0) space.
The Journal of Analysis,
Vol. 28,
Issue. 2,
p.
471.
Moslemipour, A.
Roohi, M.
Mardanbeigi, M. R.
and
Azhini, M.
2020.
Fitzpatrick transform of monotone relations in Hadamard spaces.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 28,
Issue. 2,
p.
173.
Moharami, R.
and
Eskandani, G. Zamani
2020.
An extragradient algorithm for solving equilibrium problem and zero point problem in Hadamard spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 3,
Aremu, K. O.
Jolaoso, L. O.
Izuchukwu, C.
and
Mewomo, O. T.
2020.
Approximation of common solution of finite family of monotone inclusion and fixed point problems for demicontractive multivalued mappings in CAT(0) spaces.
Ricerche di Matematica,
Vol. 69,
Issue. 1,
p.
13.
Ogwo, Grace N.
Izuchukwu, Chinedu
Aremu, Kazeem O.
and
Mewomo, Oluwatosin T.
2020.
On θ-generalized demimetric mappings and monotone operators in Hadamard spaces.
Demonstratio Mathematica,
Vol. 53,
Issue. 1,
p.
95.
Dehghan, H.
Izuchukwu, C.
Mewomo, O.T.
Taba, D.A.
and
Ugwunnadi, G.C.
2020.
Iterative algorithm for a family of monotone inclusion problems in cat(0) spaces.
Quaestiones Mathematicae,
Vol. 43,
Issue. 7,
p.
975.
TAHERNİA, Mohsen
MORADİ, Sirous
and
JAFARİ, Somayeh
2020.
The strong convergence of a proximal point algorithm in complete CAT(0) metric spaces.
Hacettepe Journal of Mathematics and Statistics,
Vol. 49,
Issue. 1,
p.
399.
Aremu, Kazeem Olalekan
Izuchukwu, Chinedu
Abass, Hammed Anuolwupo
and
Mewomo, Oluwatosin Temitope
2020.
On a Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces.
Axioms,
Vol. 9,
Issue. 4,
p.
143.
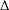 $\unicode[STIX]{x1D6E5}$-converges to a zero of the monotone operator in complete CAT(0) spaces. A strong convergence (convergence in metric) result is also presented. Finally, we consider two important special cases of monotone operators and we prove that they satisfy the range condition (see Section 4 for the definition), which guarantees the existence of the sequence generated by the proximal point algorithm.
$\unicode[STIX]{x1D6E5}$-converges to a zero of the monotone operator in complete CAT(0) spaces. A strong convergence (convergence in metric) result is also presented. Finally, we consider two important special cases of monotone operators and we prove that they satisfy the range condition (see Section 4 for the definition), which guarantees the existence of the sequence generated by the proximal point algorithm.