Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T14:17:50.258Z Has data issue: false hasContentIssue false
  • English
  • Français

The Monge-Ampère equation and warped products of higher rank

Part of: Elliptic equations and systems Global differential geometry

Published online by Cambridge University Press:  09 April 2009

Stefan Bechtluft-Sachs  and
Evangelia Samiou
Stefan Bechtluft-Sachs
Affiliation:
Department of MathematicsAmerican University of BeirutP.O. Box 11-0236 Riad El Solh Beirut 1107 2020Lebanonsb42.aub.edu.lb
Evangelia Samiou
Affiliation:
University of CyprusDepartment of Mathematics and Statistics P.O. Box 20537 1678 Nicosia [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

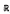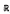We show that a warped product Mf = nf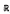 has higher rank and nonpositive curvature if and only if f is a convex solution of the Monge-Ampère equation. In this case we show that M contains a Euclidean factor.

MSC classification

Secondary: 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions 53C24: Rigidity results 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 83 , Issue 1 , August 2007 , pp. 11 - 16
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Ballmann, W., ‘Nonpositively curved manifolds of higher rank’, Ann. of Math. 122 (1985), 597–609.CrossRefGoogle Scholar
[2]Ballmann, W., Brin, M. and Eberlein, P., ‘Structure of manifolds of nonpositive curvature I’, Ann. of Math. 122 (1985), 171–203.CrossRefGoogle Scholar
[3]Ballmann, W., Brin, M. and Spatzier, R., ‘Structure of manifolds of nonpositive curvature II’, Ann. of Math. 122 (1985), 205–235.CrossRefGoogle Scholar
[4]Bemdt, J. and Samiou, E., ‘Rank rigidity, cones and curvature-homogeneous Hadamard manifolds’, Osaka J. Math. 39 (2002), 383–394.Google Scholar
[5]Boeckx, E., Kowalski, O. and Vanhecke, L., Riemannian Manifolds of conullity two (World Scientific, Singapore, 1996).CrossRefGoogle Scholar
[6]Burns, K. and Spatzier, R., ‘Manifolds of nonpositive curvature and their buildings’, Publ. Math. Inst. Hautes Études Sci. 65 (1987), 35–59.CrossRefGoogle Scholar
[7]Gutiérrez, C. E., The Monge-Ampère equation, Progr. in Nonlinear Differential Equations Appl., 44 (Birkhaüser Boston, Inc., Boston, MA, 2001).Google Scholar
[8]Kowalski, O., Tricerri, F. and Vanhecke, L., ‘Curvature-homogeneous riemannian manifolds’, J. Math. Pures Appl. 71 (1992), 471–501.Google Scholar