Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-22T22:59:29.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Meromorphic functions with one deficient value

Published online by Cambridge University Press:  09 April 2009

S. M. Shah
S. M. Shah
Affiliation:
University of Kentucky Lexington, Kentucky, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f(z) be a meromorphic function and write 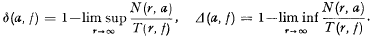Here N(r, a) and T(r, f) have their usual meanings (see [4], [5]) and 0 ≧ |a| ≧ ∞. If δ(a, f) > 0 then a is said to be an exceptional (or deficient) value in the sense of Nevanlinna (N.e.v.), and if Δ(a, f) > 0 then a is said to be an exceptional value in the sense of Varliron (V.e.v.). The Weierstrass p(z) function has no exceptional value N or V. Functions of zero order can have atmost one N.e.v. [4, p. 114], but may have more than one V.e.v. (see [6], [8]). In this note we consider functions satisfying some regularity conditions and having one and only one exceptional value V.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 3-4 , November 1969 , pp. 355 - 358
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Clunie, J., ‘On integral functions having prescribed asymptotic growth’, Canadian J. Math. 17 (1965), 396–404.CrossRefGoogle Scholar
[2]Clunie, J. and Kovari, T., ‘On integral functions having prescribed asymptotic growth II’, Canadian J. Math. 20 (1968), 7–20.CrossRefGoogle Scholar
[3]Edrei, A. and Fuchs, W. H. J., ‘Entire and meromorphic functions with asymptotically prescribed characteristic’, Canadian J. Math. 17 (1965), 383–395.CrossRefGoogle Scholar
[4]Hayman, W. K., Meromorphic Functions (Oxford Univ. Press, New York, (1964).Google Scholar
[5]Nevanlinna, R., Le théorème de Picard-Borel et la théorie des fonctions méromorphes Gauthier-Villars, Paris, 1930).Google Scholar
[6]Shah, S. M., ‘Note on a theorem of Valiron and Collingwood’, Proc. National Acad. of Sci. (India) 12 (1942), 9–12.Google Scholar
[7]Shah, S. M., ‘Entire functions with no finite deficient value’, Archive for Rational Mechanics and Analysis 26 (1967), 179–187.CrossRefGoogle Scholar
[8]Shea, D. F., ‘On the Valiron deficiencies of meromorphic functions of finite order’, Trans. Amer. Math. Soc. 124 (1966), 201–227.CrossRefGoogle Scholar
[9]Georges, Valiron, ‘Sur les valeurs déficientes des fonctions algébroides meromorphes d'ordre nul’, J. d' Analyse Math., 1 (1951), 28–42.Google Scholar