Article contents
Maximum principles for parabolic equations
Published online by Cambridge University Press: 09 April 2009
Abstract
Let u(x, t) be a smooth function in the domain Q = Ω × (0, L), Ω in 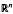 n, let Du be the spatial gradient of u(x, t) and let ∇u = (Du, u1). If u(x, t) satisfies the parabolic equation F(u, Du, D2u) = ut, we define w(x, t) by g(w) = │∇u│−1G(∇u) (g is positive and decreasing, G is concave and homogeneous of degree one) and we prove that w(x, t) attains its maximum value on the parabolic boundary of Q. If u(x, t) satisfies the equation Δu + 2h(q2) uiujuij = ut(q2 = │Du│2, 1 + 2q2h(q2) > 0) we prove that qf (u) takes its maximum value on the parabolic boundary of Q provided f satisfies a suitable condition. If u(x, t) satisfies the parabolic equation aij (Du)uij − b(x, t, u, Du) = ut (b is concave with respect to (x, t, u)) we define C(x, y, t, τ) = u(z, θ) − αu(x, t) − βu(y, τ) (0 < α, 0 < β, α + β = 1, z αx +y, θ = αt + βτ) and we prove that if C(x, y, t, r) ≤0 when x, y, z ∈ Ω2 and one of t, τ = 0, and when t, τ ∈ (0, L], and one of x, y, z, ∈ ∂Ω, then it is C(x, y, t, τ) ≤0 everywhere.
n, let Du be the spatial gradient of u(x, t) and let ∇u = (Du, u1). If u(x, t) satisfies the parabolic equation F(u, Du, D2u) = ut, we define w(x, t) by g(w) = │∇u│−1G(∇u) (g is positive and decreasing, G is concave and homogeneous of degree one) and we prove that w(x, t) attains its maximum value on the parabolic boundary of Q. If u(x, t) satisfies the equation Δu + 2h(q2) uiujuij = ut(q2 = │Du│2, 1 + 2q2h(q2) > 0) we prove that qf (u) takes its maximum value on the parabolic boundary of Q provided f satisfies a suitable condition. If u(x, t) satisfies the parabolic equation aij (Du)uij − b(x, t, u, Du) = ut (b is concave with respect to (x, t, u)) we define C(x, y, t, τ) = u(z, θ) − αu(x, t) − βu(y, τ) (0 < α, 0 < β, α + β = 1, z αx +y, θ = αt + βτ) and we prove that if C(x, y, t, r) ≤0 when x, y, z ∈ Ω2 and one of t, τ = 0, and when t, τ ∈ (0, L], and one of x, y, z, ∈ ∂Ω, then it is C(x, y, t, τ) ≤0 everywhere.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1994
References
- 5
- Cited by


