We raise a question of whether the Riesz transform on 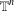$\mathbb{T}^{n}$ or 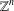$\mathbb{Z}^{n}$ is characterized by the ‘maximal semigroup symmetry’ that the transform satisfies. We prove that this is the case if and only if the dimension is one, two or a multiple of four. This generalizes a theorem of Edwards and Gaudry for the Hilbert transform on 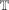$\mathbb{T}$ and 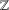$\mathbb{Z}$ in the one-dimensional case, and extends a theorem of Stein for the Riesz transform on 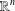$\mathbb{R}^{n}$. Unlike the 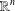$\mathbb{R}^{n}$ case, we show that there exist infinitely many linearly independent multiplier operators that enjoy the same maximal semigroup symmetry as the Riesz transforms on 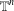$\mathbb{T}^{n}$ and 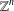$\mathbb{Z}^{n}$ if the dimension $n$ is greater than or equal to three and is not a multiple of four.