Let A be a commutative Banach algebra, D a closed derivation defined on a subalgebra Δ of A, and with range in A. The elements of Δ may be called derivable in the obvious sense. For each integer k ≦.l, denote by Δk the domain of Dk (so that Dgr;1 = Δ); it is a simple consequence of Leibniz's formula that each Δk is an algebra. The classical example of this situation is A = C(O, 1) under the supremum norm with D ordinary differentiation, and here Δk = Ck(0, 1) is a Banach algebra under the norm ∥.∥k: 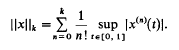Furthermore, the maximal ideals of Ak are precisely those subsets of Δk of the form M ∩ Δk where M is a maximal ideal of A, and 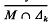= M, the bar denoting closure in A. In the present note we show how this extends to the general case.