Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-23T03:01:47.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix transformation of univalent power series

Published online by Cambridge University Press:  09 April 2009

F. W. Hartmann  and
T. H. MacGregor
F. W. Hartmann
Affiliation:
Villanova University, U.S.A.
T. H. MacGregor
Affiliation:
State University of New York at Albany, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that A = [αnk], (n, k = 0, 1, 2, …), is an indinite matrix with complex entries. A transforms a complex sequence a = {an to a complex sequence {bn = b = Aa where 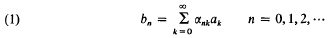assuming that the series in (1) converges. Each sequence a = {an is uniquely associated with a power series In this way the matrix A transforms a power series into a power series. Specifically, the power series (2) is mapped to the power series where the bn's are given by (1). We are only interested in matrices having the property that each power series analytic in Δ = {z: |z| < 1} maps to a power series analytic in Δ.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 18 , Issue 4 , December 1974 , pp. 419 - 435
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Cowling, V. F., ‘Summability and Analytic Continuation’, Proc. Amer. Math. Soc. 1 (1950), 536–542.CrossRefGoogle Scholar
[2]Hayman, W. K., Multivalent Functions, (Cambridge University Press, Cambridge 1958).Google Scholar
[3]Kaplan, W., ‘Close to convex schlicht functions’, Michigam Math. J. 1 (1952), 169–185.Google Scholar
[4]Krzyz, J.Lewandowski, Z., ‘On the integral of univalent functions’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 11 (1963), 447–448.Google Scholar
[5]MacGregor, T. H., ‘Certain integrals of univalent and convex functions’, Math. Zeitschr. 103 (1968), 48–54.CrossRefGoogle Scholar
[6]Maddox, I. J., Elements of Functional Analysis, (Cambridge University Press, Cambridge, 1970).Google Scholar
[7]Marx, A., ‘Untersuchungen über schlichte Abbildungen’, Math. Ann. 107 (1932), 40–67.CrossRefGoogle Scholar
[8]Nehari, Z., Conformal Mapping, (McGraw-Hill, New York, 1952).Google Scholar
[9]Reade, M. O., ‘On close-to-convex univalent functions’, Michigan Math. J. 3 (1955), 59–62.CrossRefGoogle Scholar
[10]Spacek, L., ‘Contribution à la théorie des fonctions univalentes’, Casopis Pest. Mat. 62 (1932), 12–19.Google Scholar
[11]Strohhäcker, E., ‘Beitrage zur Theorie der schlichten Funktionen’, Math. Zeitschr. 37 (1933), 356–380.CrossRefGoogle Scholar
[12]Umezawa, T., ‘On the theory of univalent functions’, Tohoku Math. J. 7 (1955), 212–228.CrossRefGoogle Scholar