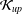Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T11:14:50.321Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ${\mathcal{K}}_{\mathit{up}}$-APPROXIMATION PROPERTY AND ITS DUALITY

Part of: Linear spaces and algebras of operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  20 November 2014

JU MYUNG KIM
JU MYUNG KIM*
Affiliation:
Department of Mathematical Sciences, Seoul National University, Seoul, 151-747, Korea email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce an approximation property (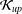${\mathcal{K}}_{\mathit{up}}$-AP, 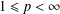$1\leq p<\infty$), which is weaker than the classical approximation property, and discover the duality relationship between the 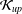${\mathcal{K}}_{\mathit{up}}$-AP and the 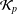${\mathcal{K}}_{p}$-AP. More precisely, we prove that for every 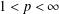$1<p<\infty$, if the dual space 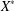$X^{\ast }$ of a Banach space 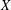$X$ has the 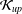${\mathcal{K}}_{\mathit{up}}$-AP, then 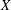$X$ has the 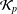${\mathcal{K}}_{p}$-AP, and if 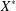$X^{\ast }$ has the 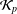${\mathcal{K}}_{p}$-AP, then 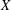$X$ has the 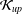${\mathcal{K}}_{\mathit{up}}$-AP. As a consequence, it follows that every Banach space has the 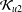${\mathcal{K}}_{u2}$-AP and that for every 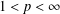$1<p<\infty$, 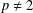$p\neq 2$, there exists a separable reflexive Banach space failing to have the 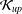${\mathcal{K}}_{\mathit{up}}$-AP.

Keywords

p-compact operatorunconditionally p-compact operatorKp-approximation propertyKup-approximation property

MSC classification

Primary: 46B28: Spaces of operators; tensor products; approximation properties
Secondary: 46B45: Banach sequence spaces 47L20: Operator ideals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 3 , June 2015 , pp. 364 - 374
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Casazza, P. G., ‘Approximation properties’, in: Handbook of the Geometry of Banach Spaces, Vol. 1 (eds. Johnson, W. B. and Lindenstrauss, J.) (Elsevier, Amsterdam, 2001), 271–316.Google Scholar
Choi, Y. S. and Kim, J. M., ‘The dual space of (L(X, Y), 𝜏 p ) and the p-approximation property’, J. Funct. Anal. 259 (2010), 2437–2454.Google Scholar
Delgado, J. M., Oja, E., Piñeiro, C. and Serrano, E., ‘The p-approximation property in terms of density of finite rank operators’, J. Math. Anal. Appl. 354 (2009), 159–164.CrossRefGoogle Scholar
Delgado, J. M., Piñeiro, C. and Serrano, E., ‘Density of finite rank operators in the Banach space of p-compact operators’, J. Math. Anal. Appl. 370 (2010), 498–505.Google Scholar
Delgado, J. M., Piñeiro, C. and Serrano, E., ‘Operators whose adjoints are quasi p-nuclear’, Studia Math. 197 (2010), 291–304.Google Scholar
Grothendieck, A., ‘Produits tensoriels topologiques et espaces nucléaires’, Mem. Amer. Math. Soc. 16 (1955).Google Scholar
Kim, J. M., ‘Unconditionally $p$ -null sequences and unconditionally $p$ -compact operators’, Studia Math., to appear.Google Scholar
Kim, J. M., ‘The approximation properties via the Grothendieck p-compact sets’, Math. Nachr. 286 (2013), 360–373.Google Scholar
Lindenstrauss, J., ‘On James’ paper “Separable conjugate spaces”’, Israel J. Math. 9 (1971), 279–284.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces I: Sequence Spaces (Springer, Berlin, 1977).Google Scholar
Megginson, R. E., An Introduction to Banach Space Theory (Springer, New York, 1998).Google Scholar
Oja, E., ‘A remark on the approximation of p-compact operators by finite-rank operators’, J. Math. Anal. Appl. 387 (2012), 949–952.CrossRefGoogle Scholar
Persson, A., ‘On some properties of p-nuclear and p-integral operators’, Studia Math. 33 (1969), 213–222.CrossRefGoogle Scholar
Sinha, D. P. and Karn, A. K., ‘Compact operators whose adjoints factor through subspaces of l p ’, Studia Math. 150 (2002), 17–33.CrossRefGoogle Scholar
Szankowski, A., ‘Subspaces without the approximation property’, Israel J. Math. 30 (1978), 123–129.Google Scholar