No CrossRef data available.
Article contents
MASS CONCENTRATION WITH MIXED NORM FOR A NONELLIPTIC SCHRÖDINGER EQUATION
Part of:
Harmonic analysis in several variables
Equations of mathematical physics and other areas of application
Partial differential equations
Published online by Cambridge University Press: 07 March 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
This paper is concerned with a mass concentration phenomenon for a two-dimensional nonelliptic Schrödinger equation. It is well known that this phenomenon occurs when the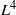 
${L}^{4} $-norm of the solution blows up in finite time. We extend this result to the case where a mixed norm of the solution blows up in finite time.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 93 , Issue 3 , December 2012 , pp. 238 - 258
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Bégout, P. and Vargas, A., ‘Mass concentration phenomena for the 
${L}^{2} $-critical nonlinear Schrödinger equation’, Trans. Amer. Math. Soc. 359 (2007), 5257–5282.CrossRefGoogle Scholar
${L}^{2} $-critical nonlinear Schrödinger equation’, Trans. Amer. Math. Soc. 359 (2007), 5257–5282.CrossRefGoogle ScholarBourgain, J., ‘Refinements of Strichartz’ inequality and applications to 2D-NLS with critical monlinearity’, Int. Math. Res. Not. 5 (1998), 253–283.CrossRefGoogle Scholar
Cazenave, T., Semilinear Schrödinger Equations, Courant Lecture Notes in Mathematics, 10 (New York University, Courant Institute of Mathematical Sciences, New York, 2003).CrossRefGoogle Scholar
Chae, M., Hong, S., Kim, J., Lee, S. and Yang, C. W., ‘On mass concentration for the ${L}^{2} $-critical nonlinear Schrödinger equations’, Comm. Partial Differential Equations 34 (4–6) (2009), 486–505.CrossRefGoogle Scholar
${L}^{2} $-critical nonlinear Schrödinger equations’, Comm. Partial Differential Equations 34 (4–6) (2009), 486–505.CrossRefGoogle ScholarChae, M., Hong, S. and Lee, S., ‘Mass concentration for the ${L}^{2} $-critical nonlinear Schrödinger equations of higher orders’, Discrete Contin. Dyn. Syst. 29 (3) (2011), 909–928.CrossRefGoogle Scholar
${L}^{2} $-critical nonlinear Schrödinger equations of higher orders’, Discrete Contin. Dyn. Syst. 29 (3) (2011), 909–928.CrossRefGoogle ScholarChrist, M. and Kiselev, A., ‘Maximal functions associated to filtrations’, J. Funct. Anal. 179 (2) (2001), 409–425.CrossRefGoogle Scholar
Keel, M. and Tao, T., ‘Endpoint Strichartz estimates’, Amer. J. Math. 120 (1998), 955–980.CrossRefGoogle Scholar
Lee, S., ‘Bilinear restriction estimates for surfaces with curvatures of different signs’, Trans. Amer. Math. Soc. 358 (2006), 3511–3533.CrossRefGoogle Scholar
Lee, S., Rogers, K. and Vargas, A., ‘Sharp null form estimates for the wave equation in ${ \mathbb{R} }^{3+ 1} $’, Int. Math. Res. Not. IMRN (2008), Art. ID rnn 096, 18 pp.CrossRefGoogle Scholar
${ \mathbb{R} }^{3+ 1} $’, Int. Math. Res. Not. IMRN (2008), Art. ID rnn 096, 18 pp.CrossRefGoogle ScholarLee, S. and Vargas, A., ‘Sharp null form estimates for the wave equation’, Amer. J. Math. 130 (5) (2008), 1279–1326.CrossRefGoogle Scholar
Moyua, A., Vargas, A. and Vega, L., ‘Restriction theorems and maximal operators related to oscillatory integrals in ${ \mathbb{R} }^{3} $’, Duke Math. J. 96 (1999), 547–574.CrossRefGoogle Scholar
${ \mathbb{R} }^{3} $’, Duke Math. J. 96 (1999), 547–574.CrossRefGoogle ScholarRogers, K. and Vargas, A., ‘A refinement of the Strichartz inequlity on the saddle and application’, J. Funct. Anal. 241 (1) (2006), 212–231.CrossRefGoogle Scholar
Sulem, C. and Sulem, P.-L., The Nonlinear Schrödinger Equation, Applied Mathematical Sciences, 139 (Springer, New York, 1999).Google Scholar
Tao, T., ‘A sharp bilinear restriction estimate for paraboloids’, Geom. Funct. Anal. 13 (2003), 1359–1384.CrossRefGoogle Scholar
Tao, T., Nonlinear Dispersive Equations, CBMS Regional Conference Series in Mathematics, 106 (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Tao, T., Vargas, A. and Vega, L., ‘A bilinear approach to the restriction and Kakeya conjecture’, J. Amer. Math. Soc. 11 (1998), 967–1000.CrossRefGoogle Scholar
Vargas, A., ‘Restriction theorems for a surface with negative curvature’, Math. Z. 249 (1) (2005), 97–111.CrossRefGoogle Scholar
You have
Access