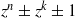Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Verger-Gaugry, Jean-Louis
2016.
On the Conjecture of Lehmer, Limit Mahler Measure of Trinomials and Asymptotic Expansions.
Uniform distribution theory,
Vol. 11,
Issue. 1,
p.
79.
Dutykh, Denys
and
Verger-Gaugry, Jean-Louis
2021.
Alphabets, rewriting trails and periodic representations in algebraic bases.
Research in Number Theory,
Vol. 7,
Issue. 4,
Flammang, Valérie
and
Voutier, Paul
2022.
Properties of trinomials of height at least 2.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 2,