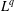Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-11T18:58:43.347Z Has data issue: false hasContentIssue false
  • English
  • Français

THE $L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS

Part of: Harmonic analysis in several variables Partial differential operators Elliptic equations and systems

Published online by Cambridge University Press:  25 April 2016

QINGQUAN DENG ,
YONG DING  and
XIAOHUA YAO
QINGQUAN DENG*
Affiliation:
School of Mathematics and Statistics, Hubei Key Laboratory of Mathematical Science, Central China Normal University, Wuhan 430079, PR China email [email protected]
YONG DING
Affiliation:
School of Mathematical Sciences, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing Normal University, Beijing 100875, PR China email [email protected]
XIAOHUA YAO
Affiliation:
School of Mathematics and Statistics, Hubei Key Laboratory of Mathematical Science, Central China Normal University, Wuhan 430079, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 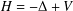$H=-\unicode[STIX]{x1D6E5}+V$ be a Schrödinger operator with some general signed potential 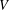$V$. This paper is mainly devoted to establishing the 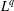$L^{q}$-boundedness of the Riesz transform 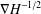$\unicode[STIX]{x1D6FB}H^{-1/2}$ for 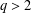$q>2$. We mainly prove that under certain conditions on 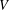$V$, the Riesz transform 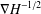$\unicode[STIX]{x1D6FB}H^{-1/2}$ is bounded on 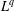$L^{q}$ for all 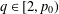$q\in [2,p_{0})$ with a given 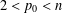$2<p_{0}<n$. As an application, the main result can be applied to the operator 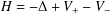$H=-\unicode[STIX]{x1D6E5}+V_{+}-V_{-}$, where 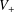$V_{+}$ belongs to the reverse Hölder class 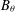$B_{\unicode[STIX]{x1D703}}$ and 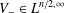$V_{-}\in L^{n/2,\infty }$ with a small norm. 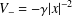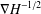In particular, if $V_{-}=-\unicode[STIX]{x1D6FE}|x|^{-2}$ for some positive number $\unicode[STIX]{x1D6FE}$, $\unicode[STIX]{x1D6FB}H^{-1/2}$ is bounded on 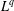$L^{q}$ for all 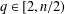$q\in [2,n/2)$ and 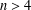$n>4$.

Keywords

Lp estimatesRiesz transformSchrödinger operatoroff-diagonal estimatereverse Hölder class

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 47F05: Partial differential operators (should also be assigned at least one other classification number in section 47) 35J10: Schrödinger operator
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 3 , December 2016 , pp. 290 - 309
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Assaad, J., ‘Riesz transform associated to Schrödinger operators with negative potentials’, Publ. Mat. 55 (2011), 123–150.CrossRefGoogle Scholar
Assaad, J. and Ouhabaz, E. M., ‘Riesz transform of Schrödinger operators on manifolds’, J. Geom. Anal. 22 (2012), 1108–1136.CrossRefGoogle Scholar
Auscher, P., ‘On necessary and sufficient conditions for L p estimates of Riesz transforms associated to elliptic operators on ℝ n and related estimates’, Mem. Amer. Math. Soc. 186(871) (2007), 1–75.Google Scholar
Auscher, P. and Ben Ali, B., ‘Maximal inequalities and Riesz transform estimates on L p spaces for Schrödinger operators with nonnegative potentials’, Ann. Inst. Fourier (Grenoble) 57 (2007), 1975–2013.CrossRefGoogle Scholar
Beceanu, M., ‘New estimates for a time-dependent Schrödinger equation’, Duke Math. J. 159 (2011), 417–477.CrossRefGoogle Scholar
Blunck, S. and Kunstmann, P. C., ‘Calderón–Zygmund theory for nonintegral operators and the H ∞ -functional calculus’, Rev. Mat. Iberoam. 19 (2003), 919–942.CrossRefGoogle Scholar
Burq, N., Planchon, F., Stalker, J. G. and Tahvildar-Zadeh, A. S., ‘Strichartz estimates for the wave and Schrödinger equations with the inverse-square potential’, J. Funct. Anal. 203 (2003), 519–549.CrossRefGoogle Scholar
Coulhon, T. and Sikora, A., ‘Gaussian heat kernel upper bounds via the Phragmen–Lindelöf theorem’, Proc. Lond. Math. Soc. (3) 96 (2008), 507–544.CrossRefGoogle Scholar
Davies, E. and Hinz, A., ‘Explicit constants for Rellich inequality in L p (𝛺)’, Math. Z. 227 (1998), 511–523.CrossRefGoogle Scholar
Deng, Q., Ding, Y. and Yao, X., ‘Characterizations of Hardy spaces associated to higher order elliptic operators’, J. Funct. Anal. 263 (2012), 604–674.CrossRefGoogle Scholar
Duong, X. T., Ouhabaz, E. M. and Yan, L., ‘Endpoint estimates for Riesz transform of magnetic Schrödinger operators’, Ark. Mat. 44 (2006), 261–275.CrossRefGoogle Scholar
Fefferman, C. L., ‘The uncertainty principle’, Bull. Amer. Math. Soc. (N.S.) 9 (1983), 129–206.CrossRefGoogle Scholar
Goldberg, M., ‘Dispersive bounds for the three-dimensional Schrödinger equation with almost critical potentials’, Geom. Funct. Anal. 16 (2006), 517–536.Google Scholar
Hassell, A. and Lin, P., ‘The Riesz transform for homogeneous Schrödinger operators on metric cones’, Rev. Mat. Iberoam. 30 (2014), 477–522.CrossRefGoogle Scholar
Hebisch, W., ‘A multiplier theorem for Schrödinger operators’, Colloq. Math. 60–61 (1990), 659–664.CrossRefGoogle Scholar
Kato, T., Perturbation Theory for Linear Operators, 2nd edn (Springer, Berlin–New York, 1980).Google Scholar
Liskevich, V., Sobol, Z. and Vogt, H., ‘On the L p -theory of C 0 -semigroups associated with second-order elliptic operators. II’, J. Funct. Anal. 193 (2002), 55–76.CrossRefGoogle Scholar
Ouhabaz, E. M., Analysis of Heat Equations on Domains, London Mathematical Society Monographs Series, 31 (Princeton University Press, Princeton, NJ, 2005).Google Scholar
Reed, M. and Simon, B., Methods of Modern Mathematical Physics. II. Fourier Analysis, Self-Adjointness (Academic Press, New York, 1975).Google Scholar
Reed, M. and Simon, B., Methods of Modern Mathematical Physics. IV. Analysis of Operators (Academic Press, New York, 1978).Google Scholar
Schechter, M., Spectra of Partial Differential Operators, 2nd edn (Elsevier Science, Amsterdam, 1986).Google Scholar
Shen, Z., ‘ L p estimates for Schrödinger operators with certain potentials’, Ann. Inst. Fourier (Grenoble) 45 (1995), 513–546.CrossRefGoogle Scholar
Sikora, A., ‘Riesz transform, Gaussian bounds and the method of wave equation’, Math. Z. 247 (2004), 643–662.CrossRefGoogle Scholar
Simon, B., ‘Schrödinger semigroups’, Bull. Amer. Math. Soc. (N.S.) 7 (1982), 447–526.CrossRefGoogle Scholar
Thangavelu, S., ‘Riesz transform and the wave equation for the Hermite operators’, Comm. Partial Differential Equations 8 (1990), 1199–1215.CrossRefGoogle Scholar
Urban, R. and Zienkiewicz, J., ‘Dimension free estimates for Riesz transforms of some Schrödinger operators’, Israel J. Math. 173 (2009), 157–176.CrossRefGoogle Scholar
Vazquez, J. L. and Zuazua, E., ‘The Hardy inequality and the asymptotic behaviour of the heat equation with an inverse-square potential’, J. Funct. Anal. 173 (2000), 103–153.CrossRefGoogle Scholar
Zhong, J., ‘Harmonic analysis for some Schrödinger type operators’, PhD Thesis, Princeton University, 1993.Google Scholar