Hostname: page-component-7b9c58cd5d-sk4tg Total loading time: 0 Render date: 2025-03-15T13:08:23.938Z Has data issue: false hasContentIssue false
  • English
  • Français

Local systems in groups

Published online by Cambridge University Press:  09 April 2009

J. A. Hulse
J. A. Hulse
Affiliation:
Mathematical Institute, University of Edinburgh, Scotland.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper we will assume that all groups are contained in some fixed but arbitrary universe. Thus the class 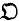of all groups becomes a set. If 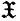is a class of groups then we assume that 1 ∈ and if H ≅ G ∈ 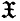then H ∈ . German capitals will be used to denote classes of groups.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 17 , Issue 4 , June 1974 , pp. 426 - 433
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Hall, P., ‘On non-strictly simple groups’, Proc. Cambridge Philos. Soc. 59 (1963), 531–553.CrossRefGoogle Scholar
[2]Hartley, B., ‘Serial subgroups of locally finite groups’, Proc. Cambridge Philos. Soc. 71 (1972), 199–201.CrossRefGoogle Scholar
[3]Hickin, K. K., ‘A class of groups whose local sequence is nonstationary’, Proc. Amer. Math. Soc. 21 (1969), 402–408.CrossRefGoogle Scholar
[4]Kuroš, A. G., The Theory of Groups, Vol. 2 (Chelsea, New York, 1956).Google Scholar
[5]Robinson, D. J. S., ‘On the theory of subnormal subgroups’, Math. Zeit. 89 (1965), 30–51.CrossRefGoogle Scholar
[6]Roseblade, J. E., ‘On certain subnormal coalition classes’, J. Algebra 1 (1964), 132–138.CrossRefGoogle Scholar
[7]Sierpinski, W., Cardinal and Ordinal Numbers (Monografie Matematyczne, Tom 34, Polish Scientific Publishers, Warsaw, 2nd Ed. Revised 1965).Google Scholar
[8]Zassenhaus, H., The Theory of Groups, (Chelsea, New York, 2nd Ed. 1958).Google Scholar