Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Samei, Ebrahim
and
Farsani, Jafar Soltani
2014.
Hyperreflexivity of bounded $$N$$ N -cocycle spaces of banach algebras.
Monatshefte für Mathematik,
Vol. 175,
Issue. 3,
p.
429.
Ebadian, A.
and
Jabbari, A.
2019.
ГИПЕРТАУБЕРОВЫ АЛГЕБРЫ, ОПРЕДЕЛЕННЫЕ ГОМОМОРФИЗМОМ БАНАХОВОЙ АЛГЕБРЫ.
Вестник КРАУНЦ. Физико-математические науки,
p.
18.
SAMEI, EBRAHIM
and
FARSANI, JAFAR SOLTANI
2020.
HYPERREFLEXIVITY CONSTANTS OF THE BOUNDED -COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS.
Journal of the Australian Mathematical Society,
Vol. 109,
Issue. 1,
p.
112.


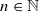 , bounded local
, bounded local 