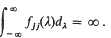Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T08:07:09.314Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear regression in continuous time

Published online by Cambridge University Press:  09 April 2009

E. J. Hannan
E. J. Hannan
Affiliation:
Department of Statistics, Institute of Advanced Studies The Australian National UniversityP.O. Box 4 Canberra, 2600, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a regression relation of the from 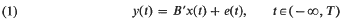wherein y(t) and x(t) are real (column) vectors of q and p components and e(t) is real and is generated by a stationary generalised vector process of q components with zero mean and covariance function (a q rowed matrix) Γ(t–s) = E{x(s)x(t)′}. (See Hannan (1970; pages 23–26, 91–94) and references therein for definitions of terms used.) We assume e(t) to be independent of x(s) for all s, t. Thus we may regard x(t) as a fixed time function and not stochastic and we shall henceforth do that. We take Γ(t) to be continuous and to correspond to an absolutely continuous spectral function with spectral density which is uniformly bounded and continuous. Then we have 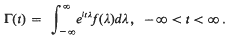We do not exclude the possibility that for theyth diagonal element, fjj, of fwe have

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 19 , Issue 2 , March 1975 , pp. 146 - 159
Copyright
Copyright © Australian Mathematical Society 1975

References

Blackman, R. B. (1965), Data Smoothing and Prediction. (Addison-Wesley, U.S.A., 1965).Google Scholar
Grenander, U. (1954), ‘On the estimation of regression coefficients in the case of autocorrelated disturbance’, Ann. Math. Statist. 25, 252–272.CrossRefGoogle Scholar
Hannan, E. J., (1968), ‘Least squares efficiency for vector time series’, J. Roy. Statist. Soc. B 30, 490–498.Google Scholar
Hannan, E. J., (1970), Multiple Time Series, (John Wiley, New York, 1970).CrossRefGoogle Scholar
Heble, M. D. (1961), ‘A regression problem concerning stationary processes’, Trans. Amer. Math. Soc. 99, 350–371.CrossRefGoogle Scholar
Kholevo, A. S. (1969), ‘On estimates of regression coefficients’, Theory of Probability and its Applications. 15, 79–104.CrossRefGoogle Scholar
Rosenblatt, M. (1959), ‘Statistical analysis of stochastic processes with stationary residual’ in “Probability and Statistics”, the Harald Cramer volume (Ed. Grenander, U.). Almqvist and Wiksells, Uppsala, 1959).Google Scholar
Rozanov, Yu. A. (1964), Appendix to Russian translation of Time Series Analysis by Hannan, E. J.. (Mir, Moscow, 1964).Google Scholar
Yaglom, A. M. (1963), ‘On the equivalence and perpendicularity of two Gaussina probability measures in function space’, Chapter 22 in Time Series Analysis (Ed. Rosenblatt, M.). (John Wiley, New York, 1963.) Since this was written there has been much work on the topic by Russian writers.Google Scholar
For a survey see Holevo, A. S. (1973), ‘On the general problem of mean estimation’ J. Multivariate Analysis. 3, 262–275.CrossRefGoogle Scholar