A recursive resampling method is discussed in this paper. Let X1, X2,…, Xn, be i.i.d. random variables with distribution function F and construct the empirical distribution function Fn. A new sample Xn+1 is drawn from Fn and the new empirical distribution function 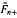1 in the wide sense, is computed from X1, X2,…, Xn, Xn+1. Then Xn+2 is drawn from 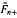1 and 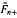2 is obtained. In this way, Xn+m and 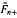m are found. It will be proved that 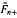m converges to a random variable almost surely as m goes to infinity and the limiting distribution is a compound beta distribution. In comparison with the usual non-recursive bootstrap, the main advantage of this procedure is a reduction in unconditional variance.