Let 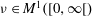$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\nu \in M^1([0,\infty [)$ be a fixed probability measure. For each dimension 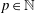$p\in \mathbb{N}$, let 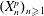$(X_n^{p})_{n\geq 1}$ be independent and identically distributed 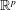$\mathbb{R}^p$-valued random variables with radially symmetric distributions and radial distribution $\nu $. We investigate the distribution of the Euclidean length of 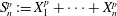$S_n^{p}:=X_1^{p}+\cdots + X_n^{p}$ for large parameters $n$ and 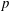$p$. Depending on the growth of the dimension 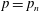$p=p_n$ we derive by the method of moments two complementary central limit theorems (CLTs) for the functional 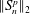$\| S_n^{p}\| _2$ with normal limits, namely for 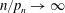$n/p_n \to \infty $ and 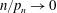$n/p_n \to 0$. Moreover, we present a CLT for the case 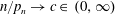$n/p_n \to c\in \, (0,\infty )$. Thereby we derive explicit formulas and asymptotic results for moments of radial distributed random variables on 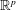$\mathbb{R}^p$. All limit theorems are also considered for orthogonal invariant random walks on the space 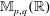$\mathbb{M}_{p,q}(\mathbb{R})$ of 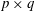$p\times q$ matrices instead of 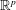$\mathbb{R}^p$ for 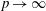$p\to \infty $ and some fixed dimension 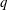$q$.