No CrossRef data available.
Article contents
The limit theorem for aperiodic discrete renewal processes
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A discrete renewal process is a sequence {X4} of independently and inentically distributed random variables which can take on only those values which are positive integral multiples of a positive real number δ. For notational convenience we take δ = 1 and write 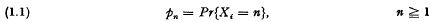 where
where 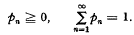 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1964
References
[1]Doob, J. L., Renewal theory from the point of view of the theory of probability, Trans. Amer. Math. Soc. 63, 422–38 (1948).CrossRefGoogle Scholar
[3]Erdös, P., Feller, W., and Pollard, H., A theorem on power series, Bull. Amer. Math. Soc. 55, 201–204 (1949).CrossRefGoogle Scholar
[4]Feller, W., A simple proof for renewal theorems, Comm. Pure Appl. Math. 14, 285–293 (1961).CrossRefGoogle Scholar
[5]Kolmogorov, A., Anfangagründe der Theorie der Markoffschen Ketten mit unendlich vielen möglichen Zuständen, Mat. Sbornik. N.S. 1, 607–610 (1936).Google Scholar


