Left restriction semigroups are the unary semigroups that abstractly characterize semigroups of partial maps on a set, where the unary operation associates to a map the identity element on its domain. This paper is the sequel to two recent papers by the author, melding the results of the first, on membership in the variety 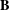$\mathbf{B}$ of left restriction semigroups generated by Brandt semigroups and monoids, with the connection established in the second between subvarieties of the variety 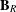$\mathbf{B}_{R}$ of two-sided restriction semigroups similarly generated and varieties of categories, in the sense of Tilson. We show that the respective lattices 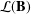${\mathcal{L}}(\mathbf{B})$ and 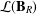${\mathcal{L}}(\mathbf{B}_{R})$ of subvarieties are almost isomorphic, in a very specific sense. With the exception of the members of the interval 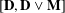$[\mathbf{D},\mathbf{D}\vee \mathbf{M}]$, every subvariety of 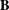$\mathbf{B}$ is induced from a member of 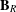$\mathbf{B}_{R}$ and vice versa. Here 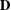$\mathbf{D}$ is generated by the three-element left restriction semigroup 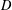$D$ and 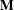$\mathbf{M}$ is the variety of monoids. The analogues hold for pseudovarieties.