Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T09:00:45.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice isomorphisms of associative algebras

Published online by Cambridge University Press:  09 April 2009

D. W. Barnes
D. W. Barnes
Affiliation:
University of Sydney
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

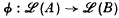Let A be an associative algebra over the field F. We denote by ℒ(A) the lattice of all subalgebras of A. By an ℒ-isomorphism (lattice isomorphism) of the algebra A onto an algebra B over the same field, we mean an isomorphism of ℒ(A) onto ℒ(B). We investigate the extent to which the algebra B is determined by the assumption that it is ℒ-isomorphic to a given algebra A. In this paper, we are mainly concerned with the case in which A is a finite- dimensional semi-simple algebra.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 6 , Issue 1 , February 1966 , pp. 106 - 121
Copyright
Copyright © Australian Mathematical Society 1966

References

[1]Ancochea, G., “On semi-automorphisms of division algebras”, Annals of Math. 48 (1947), 147–153.CrossRefGoogle Scholar
[2]Artin, E., Nesbitt, C. J. and Thrall, R. M., Rings with minimum condition (University of Michigan Press, Ann Arbor, 1944).Google Scholar
[3]Barnes, D. W., “On the radical of a ring with minimum condition”, J. Aust. Math. Soc. 5 (1965), 234–236.CrossRefGoogle Scholar
[4]Hua, L. K., “On the automorphisms of a sfield”, Proc. Nat. Acad. Sci. USA. 35 (1949), 386–389.CrossRefGoogle ScholarPubMed
[5]Jacobson, N., Structure of rings, Am. Math. Soc. Colloquium Publications XXXVII, 1956.Google Scholar
[6]Kaplansky, I., “Semi-automorphisms of rings”, Duke Math. J. 14 (1947), 521–525.CrossRefGoogle Scholar