Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T18:57:57.656Z Has data issue: false hasContentIssue false
  • English
  • Français

The last problem of Harald Bohr

Part of: Series expansions

Published online by Cambridge University Press:  09 April 2009

Jean-Pierre Kahane
Jean-Pierre Kahane
Affiliation:
Départment de Mathématique, University of Paris-Sud, 91405 Orsay, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The first and last papers of Harald Bohr deal with ordinary Dirichlet series 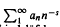and their order (or Lindelöf) function μ(σ) (= inf{α;f(σ + it) + 0(|t|α)}). The Lindelöf hypothesis is μ(σ) = inf(0, ½ − t) when an = (−1)n. Are there ordinary Dirichlet series with −l < μ′ (σ) < 0 for some σ? A negative answer would imply Lindelöf's hypothesis. This is the last problem of Harald Bohr. This paper gives (1) a review on Bohr's results on ordinary Dinchlet series; (2) a review on results of the author and of Queffelec on “almost sure” and “quasi sure” properties of series with the solution of a previous problem of Bohr; (3) the following answer to the last problem: μ′(σ) can approach − ½, and necessarily μ(σ + μ(σ) + ½) = 0. The characterization of the order functions of ordinary Dirichlet series remains an open question.

MSC classification

Secondary: 30B50: Dirichlet series and other series expansions, exponential series
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 47 , Issue 1 , August 1989 , pp. 133 - 152
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Bohr, H., Bidrag til de Dirichlet'ske Raekkers Theori, (Dissertation, Copenhagen 1910) (1A3 and in English translation III S1 in Collected Mathematical Works of Harald Bohr)Google Scholar
[2]Bohr, H., ‘On the convergence problem for Dirichiet series’, Dan. Mat. Fys. Medd. 25 6 (1946), 1–18. (IA17 in Collected Mathematical Works of Harald Bohr)Google Scholar
[3]Bohr, H., ‘Zur Theorie der Dirichletschen Reichen’, Math. Z. 52 (1950), 709–722. (IA18 in Collected Mathematical Works of Harald Bohr)Google Scholar
[4]Bohr, H., ‘On the summability function and the order function of Dirichiet series’, Dan. Mat. Fys. Medd. 274 (1952), 1–39. (1A22 in Collected Mathematical Works of Harald Bohr)Google Scholar
[5]Hardy, G. H. and Riesz, Marcel, The general theory of Dirichiet's series, (Cambridge Tracts in Math, and Math. Physics) 18 (1945).Google Scholar
[6]Helson, H., ‘Convergent Dirichlet series’, Ark Mat. 4 (1962), 501–510.CrossRefGoogle Scholar
[7]Helson, H., ‘Convergence of Dinchlet series’, L'analyse harmonique dans le domaine complexe, (Table Ronde, C.N.R.S., Montpellier 1972, Lecture Notes in Math., vol.336, Springer-Verlag 1973, pp. 153–160).Google Scholar
[8]Kahane, J. P., ‘Sur les series de Dirichlet ’, C.R. Acad. Sci. Paris 276 (1973), 739–742.Google Scholar
[9]Kahane, J. P., ‘Sur les polynomes à coefficients unimodulaires’, Bull. London Math. Soc. 12 (1980), 321–342.CrossRefGoogle Scholar
[10]Montgomery, H. L. and Vaughan, R. C., ‘Hilbert's inequality’, J. London Math. Soc. 8 (1974), 73–82.CrossRefGoogle Scholar
[11]Queffelec, H., ‘Propriétés presque s res et quasi-s res des séries de Dirichlet et des produitsd ' Euler’, Canad. J. Math. 32 (1980), 531–558.CrossRefGoogle Scholar