Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T16:16:44.294Z Has data issue: false hasContentIssue false
  • English
  • Français

LANDAU’S THEOREM, FIELDS OF VALUES FOR CHARACTERS, AND SOLVABLE GROUPS

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  23 December 2016

MARK L. LEWIS Open the ORCID record for MARK L. LEWIS [Opens in a new window]
MARK L. LEWIS*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When 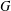$G$ is a finite solvable group, we prove that 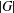$|G|$ can be bounded by a function in the number of irreducible characters with values in fields where 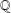$\mathbb{Q}$ is extended by prime power roots of unity. This gives a character theory analog for solvable groups of a theorem of Héthelyi and Külshammer that bounds the order of a finite group in terms of the number of conjugacy classes of elements of prime power order. In particular, we obtain for solvable groups a generalization of Landau’s theorem.

Keywords

Landau’s theoremsolvable groupsirreducible charactersfields of value

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20E45: Conjugacy classes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 1 , February 2018 , pp. 37 - 43
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Gajendragadkar, D., ‘A characteristic class of characters of finite p-separable groups’, J. Algebra 59(2) (1979), 237–259.CrossRefGoogle Scholar
Héthelyi, L. and Külshammer, B., ‘Elements of prime power order and their conjugacy classes in finite groups’, J. Aust. Math. Soc. 78(2) (2005), 291–295.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, San Diego, CA, 1976).Google Scholar
Isaacs, I. M., ‘Abelian normal subgroups of M-groups’, Math. Z. 182(2) (1983), 205–221.CrossRefGoogle Scholar
Isaacs, I. M., ‘Characters of 𝜋-separable groups’, J. Algebra 86(1) (1984), 98–128.CrossRefGoogle Scholar
Isaacs, I. M., ‘Characters of solvable groups’, in: The Arcata Conference on Representations of Finite Groups (Arcata, CA, 1986), Proceedings of Symposia in Pure Mathematics, 47, Part 1 (American Mathematical Society, Providence, RI, 1987), 103–109.CrossRefGoogle Scholar
Isaacs, I. M., ‘Characters and Hall subgroups of groups of odd order’, J. Algebra 157(2) (1993), 548–561.CrossRefGoogle Scholar
Isaacs, I. M., ‘The 𝜋-character theory of solvable groups’, J. Aust. Math. Soc. Ser. A 57(1) (1994), 81–102.CrossRefGoogle Scholar
Landau, E., ‘Über die Klassenzahl der binären quadratischen Formen von negativer Discriminante’, Math. Ann. 56(4) (1903), 671–676.CrossRefGoogle Scholar
Lewis, M. L., ‘ $B_{\unicode[STIX]{x1D70B}}$ -characters and quotients’, 2016. arXiv:1609.02029.Google Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar