No CrossRef data available.
Article contents
Iterative criteria for bounds on the growth of positive solutions of a delay differential equation
Part of:
Qualitative theory
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Following Terry (Pacific J. Math. 52 (1974), 269–282), the positive solutions of eauqtion (E): 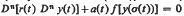 are classified according to types Bj. We denote
are classified according to types Bj. We denote 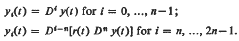 A neccessary condition is given for a Bk-solution y(t) of (E) to satisfy y2k(t) ≥ m(t) > 0. In the case m(t) = C > 0, we obtain a sufficient condition for all solutions of (E) to be oscillatory.
A neccessary condition is given for a Bk-solution y(t) of (E) to satisfy y2k(t) ≥ m(t) > 0. In the case m(t) = C > 0, we obtain a sufficient condition for all solutions of (E) to be oscillatory.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1978
References
REFERENCES
Burton, T. and Grimmer, R. (1972), “Oscillatory solutions of x″(t)+a(t)f[x(g(t))] = 0”, Delay and Functional Differential Equations and their Applications, 335–342 (Academic Press, New York).Google Scholar
Ladas, G. (1971), “On principal solutions of nonlinear differential equations”, J. Math. Anal. Appl. 36, 103–109.CrossRefGoogle Scholar
Terry, R. D. (1974), “Oscillatory properties of a delay differential equation of even order”, Pacific J. Math. 52, 269–282.CrossRefGoogle Scholar
Terry, R. D. (1975), “Some oscillation criteria for delay differential equations of even order”, SIAM J. Appl. Math. 28, 319–334.CrossRefGoogle Scholar
Terry, R. D. (1976), “Oscillatory and asymptotic properties of homogeneous and nonhomogeneous delay differential equations of even order”, J. Austral. Math. Soc. 22 (Ser. A), 282–304.CrossRefGoogle Scholar


