No CrossRef data available.
Article contents
The iterated equation of generalized axially symmetric potential theory, VI General solutions
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The iterated equation of generalized axially symmetric potential theory [1] is the equation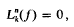 
where, in its simplest form, the operator Lk is defined by 
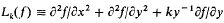the function f 
f(x, y) being assumed to belong to the class of C2n functions and the parameter l to take any real value. In appropriate circumstances, which will be indicated later, the operator can be generalized but as this can be done without altering the methods used, the operator will be taken in the form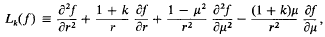 
where r, θ are polar coordinates such that x = r cos θ, y = r sin μ = cosθ.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 18 , Issue 3 , November 1974 , pp. 318 - 327
- Copyright
- Copyright © Australian Mathematical Society 1974
References
[1]Weinstein, A., ‘Generalized axially symmetric potential theory’, Bull. Amer. Math. Soc. 59 (1953), 20–28.CrossRefGoogle Scholar
[2]Burns, J. C., ‘The iterated equation of generalized axially symmetric potential theory, I. Particular solutions’, J. Austral. Math. Soc. 7 (1967), 263–276.CrossRefGoogle Scholar
[3]Weinstein, A., ‘On a class of partial differential equations of even order’, Ann. Mat. Pura Appl. 39 (1955), 245–254.CrossRefGoogle Scholar
[4]Payne, L. E., ‘Representation formulas for solutions of a class of partial differential equation’, J. Math. and Phys. 38 (1959), 145–149.CrossRefGoogle Scholar
[5]Burns, J. C., ‘The iterated equation of generalized axially symmetric potential theory, II. General solutions of Weinstein' type’, J. Austral. Math. Soc. 7 (1967), 277–289.CrossRefGoogle Scholar
You have
Access