Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rbragg, L.
1974.
Related non-homogeneous partial differential equations.
Applicable Analysis,
Vol. 4,
Issue. 2,
p.
161.
Rogers, C.
1974.
On reduction properties in the theory of lubrication.
Journal of Engineering Mathematics,
Vol. 8,
Issue. 3,
p.
209.
Rogers, C.
Cekirge, H. M.
and
Askar, A.
1977.
Electromagnetic wave propagation in non-linear dielectric media.
Acta Mechanica,
Vol. 26,
Issue. 1-4,
p.
59.
Bragg, L. R.
1981.
Vector Lifting and Factorable Differential Operators.
SIAM Journal on Mathematical Analysis,
Vol. 12,
Issue. 5,
p.
722.
Bragg, L.R
1981.
Abstract Cauchy problems that involve a product of two Euler-Poisson-Darboux operators.
Journal of Differential Equations,
Vol. 41,
Issue. 3,
p.
426.
Bragg, L. R.
1990.
The iterated abstract euler-poisson-darboux problem for negative values of the parameter.
Applicable Analysis,
Vol. 37,
Issue. 1-4,
p.
213.
Urinov, A. K.
and
Karimov, Sh. T.
2020.
On the Cauchy Problem for the Iterated Generalized Two-axially Symmetric Equation of Hyperbolic Type.
Lobachevskii Journal of Mathematics,
Vol. 41,
Issue. 1,
p.
102.


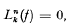
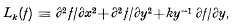
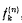 except that when
except that when 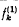 . It is easily shown [2, 3] that
. It is easily shown [2, 3] that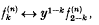
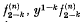 is a solution of (1).
is a solution of (1).