Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T22:57:19.019Z Has data issue: false hasContentIssue false
  • English
  • Français

The inversion of a transform related to the Laplace transform and to heat conduction*

Published online by Cambridge University Press:  09 April 2009

David V. Widder
David V. Widder
Affiliation:
Harvard University and University of Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper [7] the author considered, among other things, the integral transform 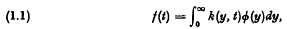where is the fundamental solution of the heat equation There we gave a physical interpretation of the transform (1.1). Here we shall choose a slightly different interpretation, more convenient for our present purposes. If then u(O, t) = f(t). That is, the function f(t) defined by equation (1.1) is the temperature at the origin (x = 0) of an infinite bar along the x-axis t seconds after it was at a temperature defined by the equation .

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 1 , February 1964 , pp. 1 - 14
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Boas, R. P., Entire Functions, Academic Press (1954).Google Scholar
[2]Ford, L. R., Differential Equations, McGraw-Hill (1955).Google Scholar
[3]Rosenbloom, P. C. and Widder, D. V., Expansions in terms of heat polynomials and associated functions, Trans. Amer. Math. Soc., 92 (1959), 220–266.CrossRefGoogle Scholar
[4]Staff of the Bateman Manuscript Project, Tables of Integral Transforms, vol 1, McGraw-Hill (1954).Google Scholar
[5]Widder, D. V., The Laplace Transform, Princeton University Press (1946).Google Scholar
[6]Widder, D. V., The Convolution Transform Princeton University Press (1955).Google Scholar
[7]Widder, D. V., Integral transforms related to heat conduction, Annali di Matematica, 42 (1956), 279–305.Google Scholar