Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T16:34:00.059Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse semigroups determined by their lattices of inverse subsemigroups

Part of: Semigroups Algebraic structures

Published online by Cambridge University Press:  09 April 2009

P. R. Jones
P. R. Jones
Affiliation:
Department of Mathematics, Monash University, Clayton, Victoria 3168, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

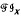In a previous paper ([14]) the author showed that a free inverse semigroup is determined by its lattice 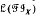of inverse subsemigroups, in the sense that for any inverse semigroup T,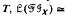 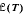implies 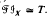. (In fact, the lattice isomorphism is induced by an isomorphism of 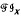upon T.) In this paper the results leading up to that theorem are generalized (from completely semisimple to arbitrary inverse semigroups) and applied to various classes, including simple, fundamental and E-unitary inverse semigroups. In particular it is shown that the free product of two groups in the category of inverse semigroups is determined by its lattice of inverse subsemigroups.

MSC classification

Secondary: 20M10: General structure theory 08A30: Subalgebras, congruence relations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 30 , Issue 3 , February 1981 , pp. 321 - 346
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Aršinov, M. N., ‘Projectivity of a free product and isomorphisms of groups’, Sibirsk. Mat. Ž. 11 (1970), 12–19 (in Russian).Google Scholar
[2]Birkhoff, G., Lattice theory (3 rd ed., A.M.S. Colloquium Publications, Amer. Math. Soc., Providence, R.I., 1967).Google Scholar
[3]Clifford, A. H. and Preston, G. B., Algebraic theory of semigroups (Math. Surveys 7, Vol. I, 1961, Vol. II, 1967, Amer. Math. Soc., Providence, R.I.).CrossRefGoogle Scholar
[4]Eberhart, C., ‘Elementary orthodox semigroups’, Proc. Symposium on Inverse Semigroups and their Generalizations, Northern Illinois University, 1973, 23–33.Google Scholar
[5]Eršova, T., ‘Monogenically inverse semigroups’, Ural. Gos. Univ. Mat. Zap. 8 (1971) tetrad'l, 30–33 (in Russian).Google Scholar
[6]Eršova, T., ‘Determinability of monogenically inverse semigroups by the lattice of inverse subsemigroups’, Ural. Gos. Univ. Mat. Zap. 8 (1971), tetrad'l, 34–49 (in Russian).Google Scholar
[7]Gluskin, L. M., ‘Elementary generalized groups’, Mat. Sb. 41(83) (1957), 23–26 (in Russian).Google Scholar
[8]Green, D. G., ‘Extensions of a semilattice by an inverse semigroup’, Bull. Austral. Math. Soc. 9 (1973), 21–31.CrossRefGoogle Scholar
[9]Hall, M. Jr, The theory of groups (Macmillan, New York, 1959).Google Scholar
[10]Holmes, C. S., ‘Projectivities of free products’, Rend. Sem. Mat. Univ. Padova 42 (1969), 341–387.Google Scholar
[11]Howie, J. M., ‘The maximum idempotent-separating congruence on an inverse semigroup’, Proc. Edinburgh Mat. Soc. (2) 14 (1964), 71–79.CrossRefGoogle Scholar
[12]Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
[13]Jones, P. R., ‘Basis properties for inverse semigroups’, J. Algebra 50 (1978), 135–152.CrossRefGoogle Scholar
[14]Jones, P. R., ‘Lattice isomorphisms of inverse semigroups’, Proc. Edinburgh Math. Soc. 21 (1978), 149–157.CrossRefGoogle Scholar
[15]Jones, P. R., ‘Semimodular inverse semigroups’, J. London Math. Soc. 17 (1978), 446–456.CrossRefGoogle Scholar
[16]Jones, P. R., ‘Distributive inverse semigroups’, J. London Math. Soc. 17 (1978), 457–466.CrossRefGoogle Scholar
[17]Jones, P. R., ‘Lattice isomorphisms of distributive inverse semigroups’, Quart. J. Math. Oxford Ser. 30 (1979), 301–314.CrossRefGoogle Scholar
[18]Knox, N., On the inverse semigroup coproduct of an arbitrary non-empty collection of groups (Ph.D. Thesis, Tennessee State University, Tennessee, 1976).Google Scholar
[19]Kočin, B. P., ‘The structure of inverse ideal-simple ω-semigroups’, Vestnik Leningrad Univ. Math. 23, No. 7 (1968), 41–50 (in Russian).Google Scholar
[20]McAlister, D. B., ‘Groups, semilattices and inverse semigroups, II’, Trans. Amer. Math. Soc. 196 (1974), 351–370.CrossRefGoogle Scholar
[21]McAlister, D. B., ‘Inverse semigroups generated by a pair of subgroups’, Proc. Royal Soc. Edinburgh 77A (1977), 9–22.CrossRefGoogle Scholar
[22]Munn, W. D., ‘Uniform semilattices and bisimple inverse semigroups’, Quart. J. Math. Oxford Ser. 17 (1966), 151–159.CrossRefGoogle Scholar
[23]Munn, W. D., ‘Regular ω-semigroups’, Glasgow Math. J. 9 (1968), 46–66.CrossRefGoogle Scholar
[24]Munn, W. D., ‘Fundamental inverse semigroups’, Quart. J. Math. Oxford Ser. 21 (1970), 157–170.CrossRefGoogle Scholar
[25]Munn, W. D., ‘On simple inverse semigroups’, Semigroup Forum 1 (1970), 63–74.CrossRefGoogle Scholar
[26]Ore, O., ‘Structures and group theory’, II, Duke Math. J. 4 (1938), 247–269.CrossRefGoogle Scholar
[27]Preston, G. B., ‘Inverse semigroups: some open questions’, Proc. Symposium on Inverse Semigroups and their Generalizations, Northern Illinois University, 1973, 122–139.Google Scholar
[28]Reilly, N. R., ‘Congruences on a bisimple inverse semigroup in terms of RP-systems’, Proc. London Math. Soc. (3) 23 (1971), 99–127.CrossRefGoogle Scholar
[29]Reilly, N. R. and Munn, W. D., ‘E-urntary congruences on inverse semigroups’, Glasgow Math. J. 17 (1976), 57–75.CrossRefGoogle Scholar
[30]Sadovskii, E. L., ‘Über die Strukturisomorphismen von Friegruppen’, Doklady Akad. Nauk SSSR 23 (1941), 171–174.Google Scholar
[31]Sadovskii, E. L., ‘On structural isomorphisms of free products of groups’, Mat. Sb. 21 (63) (1947), 63–82 (in Russian).Google Scholar
[32]Sevrin, L. N., ‘Fundamental questions in the theory of projectivities in semilattices’, Mat. Sb. 66 (108) (1965), 568–597 (in Russian).Google Scholar
[33]Suzuki, M., Structure of a group and the structure of its lattice of subgroups (Springer, 1956).CrossRefGoogle Scholar