Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Erdös, P.
Milner, E. C.
and
Rado, R.
1976.
Families of sets whose pairwise intersections have prescribed cardinals or order types.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 80,
Issue. 2,
p.
215.
Rado, Richard
1977.
Higher Combinatorics.
p.
69.
1977.
Combinatorial Set Theory.
Vol. 91,
Issue. ,
p.
196.
Erdös, P
and
Szemerédi, E
1978.
Combinatorial properties of systems of sets.
Journal of Combinatorial Theory, Series A,
Vol. 24,
Issue. 3,
p.
308.
Williams, N. H.
1978.
Chain conditions and the existence of delta-families.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 83,
Issue. 2,
p.
167.
Erdös, P.
1979.
OLD AND NEW PROBLEMS IN COMBINATORIAL ANALYSIS AND GRAPH THEORY.
Annals of the New York Academy of Sciences,
Vol. 319,
Issue. 1,
p.
177.
Erdős, P.
1981.
On the combinatorial problems which I would most like to see solved.
Combinatorica,
Vol. 1,
Issue. 1,
p.
25.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
Williams, N. H.
1988.
An order property for families of sets.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 44,
Issue. 3,
p.
294.
Axenovich, M.
Fon-Der-Flaass, D.
and
Kostochka, A.
1995.
On set systems without weak 3-Δ-subsystems.
Discrete Mathematics,
Vol. 138,
Issue. 1-3,
p.
57.
Deuber, W.A
Erdős, P
Gunderson, D.S
Kostochka, A.V
and
Meyer, A.G
1997.
Intersection Statements for Systems of Sets.
Journal of Combinatorial Theory, Series A,
Vol. 79,
Issue. 1,
p.
118.
Kostochka, Alexandr V.
2000.
Numbers, Information and Complexity.
p.
143.
Hajnal, András
2013.
The Mathematics of Paul Erdős II.
p.
379.
Arman, Andrii
Kay, Bill
and
Rödl, Vojtěch
2019.
A note on weak delta systems.
Discrete Mathematics,
Vol. 342,
Issue. 11,
p.
3034.
Naslund, Eric
2023.
Upper Bounds For Families Without Weak Delta-Systems.
Combinatorica,
Vol. 43,
Issue. 4,
p.
729.
Frankl, Peter
Pach, Janos
and
Pálvölgyi, Dömötör
2023.
Odd-Sunflowers.
p.
441.
Frankl, Peter
Pach, János
and
Pálvölgyi, Dömötör
2024.
Odd-sunflowers.
Journal of Combinatorial Theory, Series A,
Vol. 206,
Issue. ,
p.
105889.
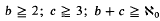 the least cardinal a = fδ(b, c) was determined which has the property that every (a, < b)-system contains a δ(c)-subsystem.
the least cardinal a = fδ(b, c) was determined which has the property that every (a, < b)-system contains a δ(c)-subsystem.