Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T00:01:08.270Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS

Part of: Geometric function theory

Published online by Cambridge University Press:  16 July 2015

MD FIROZ ALI  and
A. VASUDEVARAO
MD FIROZ ALI
Affiliation:
Department of Mathematics, IIT Kharagpur, Kharagpur-721 302, West Bengal, India email [email protected]
A. VASUDEVARAO*
Affiliation:
Department of Mathematics, IIT Kharagpur, Kharagpur-721 302, West Bengal, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a normalized analytic function 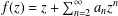$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ in the unit disk 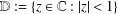$\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$, the estimate of the integral means

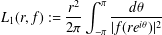$$\begin{eqnarray}L_{1}(r,f):=\frac{r^{2}}{2{\it\pi}}\int _{-{\it\pi}}^{{\it\pi}}\frac{d{\it\theta}}{|f(re^{i{\it\theta}})|^{2}}\end{eqnarray}$$
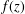is an important quantity for certain problems in fluid dynamics, especially when the functions $f(z)$ are nonvanishing in the punctured unit disk 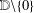$\mathbb{D}\setminus \{0\}$. Let 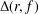${\rm\Delta}(r,f)$ denote the area of the image of the subdisk 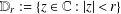$\mathbb{D}_{r}:=\{z\in \mathbb{C}:|z|<r\}$ under 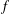$f$, where 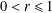$0<r\leq 1$. In this paper, we solve two extremal problems of finding the maximum value of 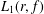$L_{1}(r,f)$ and 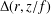${\rm\Delta}(r,z/f)$ as a function of $r$ when 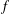$f$ belongs to the class of 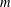$m$-fold symmetric starlike functions of complex order defined by a subordination relation. One of the particular cases of the latter problem includes the solution to a conjecture of Yamashita, which was settled recently by Obradović et al. [‘A proof of Yamashita’s conjecture on area integral’, Comput. Methods Funct. Theory13 (2013), 479–492].

Keywords

analyticunivalentstarlikespiral-likeDirichlet-finitehypergeometric functionsarea integralsubordination relation

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.) 30C70: Extremal problems for conformal and quasiconformal mappings, variational methods
Secondary: 33C05: Classical hypergeometric functions, $_2F_1$ 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 3 , December 2015 , pp. 315 - 333
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Anh, V. V., ‘k-fold symmetric starlike univalent functions’, Bull. Aust. Math. Soc. 32(3) (1985), 419–436.CrossRefGoogle Scholar
Clunie, J. G., ‘On meromorphic Schlicht functions’, J. Lond. Math. Soc. (2) 34 (1959), 215–216.CrossRefGoogle Scholar
Clunie, J. G. and Keogh, F. R., ‘On starlike and convex Schlicht functions’, J. Lond. Math. Soc. (2) 35 (1960), 229–233.CrossRefGoogle Scholar
Duren, P. L., Univalent Functions, Grundlehren der mathematischen Wissenschaften, 259 (Springer, New York–Berlin–Heidelberg–Tokyo, 1983).Google Scholar
Golusin, G., ‘On some estimates for functions which map the circle conformally and univalently’, Recueil Math. Moscow 36 (1929), 152–172.Google Scholar
Gromova, L. and Vasil’ev, A., ‘On integral means of star-like functions’, Proc. Indian Acad. Sci. Math. Sci. 112(4) (2002), 563–570.CrossRefGoogle Scholar
Janowski, W., ‘Some extremal problems for certain families of analytic functions’, Ann. Polon. Math. 28 (1973), 297–326.CrossRefGoogle Scholar
Libera, R. J., ‘Univalent 𝛼-spiral functions’, Canad. J. Math. 19 (1967), 449–456.CrossRefGoogle Scholar
Littlewood, J. E., ‘On inequalities in the theory of functions’, Proc. London Math. Soc. (3) 23 (1925), 481–519.CrossRefGoogle Scholar
Miller, S. S. and Mocanu, P. T., Differential Subordinations: Theory and Applications, Monographs and Textbooks in Pure and Applied Mathematics, 225 (Marcel Dekker, New York, 2000).CrossRefGoogle Scholar
Nasr, M. A. and Aouf, M. K., ‘Radius of convexity for the class of starlike functions of complex order’, Bull. Fac. Sci. Assiut Univ. A 12(1) (1983), 153–159.Google Scholar
Nevanlinna, R., ‘Über die konforme Abbildung von Sterngebieten’, Öfvers. Finska Vetensk. Soc. F̈orh. 63A (1921), 1–21.Google Scholar
Noshiro, K., ‘On the theory of Schlicht functions’, J. Fac. Sci. Hokkaido Univ. I 2 (1934), 129–155.Google Scholar
Obradović, M., Ponnusamy, S. and Wirths, K.-J., ‘A proof of Yamashita’s conjecture on area integral’, Comput. Methods Funct. Theory 13 (2013), 479–492.CrossRefGoogle Scholar
Obradović, M., Ponnusamy, S. and Wirths, K.-J., ‘Integral means and Dirichlet integral for analytic functions’, Math. Nachr. 288 (2015), 334–342.CrossRefGoogle Scholar
Padmanabhan, K. S., ‘On certain classes of starlike functions in the unit disk’, J. Indian Math. Soc. 32 (1968), 89–103.Google Scholar
Ponnusamy, S., Sahoo, S. K. and Sharma, N. L., ‘Maximal area integral problem for certain class of univalent analytic functions’, Mediterr. J. Math., to appear. Published online 12 February 2015.CrossRefGoogle Scholar
Ponnusamy, S. and Wirths, K.-J., ‘On the problem of Gromova and Vasil’ev on integral means, and Yamashita’s conjecture for spirallike functions’, Ann. Acad. Sci. Fenn. AI 39 (2014), 721–731.Google Scholar
Robertson, M. S., ‘On the theory of univalent functions’, Ann. of Math. (2) 37 (1936), 374–408.CrossRefGoogle Scholar
Robertson, M. S., ‘Quasi-subordination and coefficient conjectures’, Bull. Amer. Math. Soc. (N.S.) 76 (1970), 1–9.CrossRefGoogle Scholar
Sahoo, S. K. and Sharma, N. L., ‘On maximal area integral problem for analytic functions in the starlike family’, J. Class. Anal. 6 (2015), 73–84.CrossRefGoogle Scholar
Silverman, H., ‘Subclass of starlike functions’, Rev. Roumaine Math. Pures Appl. 33 (1978), 1093–1099.Google Scholar
Singh, R., ‘On a class of starlike functions’, J. Indian Math. Soc. 32 (1968), 208–213.Google Scholar
Singh, R. and Singh, V., ‘On a class of bounded starlike functions’, Indian J. Pure Appl. Math. 5 (1974), 733–754.Google Scholar
Špaček, L., ‘Contribution à la théorie des fonctions univalentes’, Časopis Pěst. Mat. Fys. 62 (1933), 12–19.CrossRefGoogle Scholar
Vasil’ev, A., ‘Univalent functions in two-dimensional free boundary problems’, Acta Appl. Math. 79(3) (2003), 249–280.CrossRefGoogle Scholar
Vasil’ev, A. and Markina, I., ‘On the geometry of Hele-Shaw flows with small surface tension’, Interfaces Free Bound. 5(2) (2003), 183–192.CrossRefGoogle Scholar
Yamashita, S., ‘Area and length maxima for univalent functions’, Bull. Aust. Math. Soc. 41 (1990), 435–439.CrossRefGoogle Scholar