Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-25T17:05:32.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities relating different definitions of discrepancy

Published online by Cambridge University Press:  09 April 2009

C. J. Smyth
C. J. Smyth
Affiliation:
Department of Pure Mathematics and Mathematical Statistics University of Cambridge16 Mill Lane Cambridge CB2 ISB, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

LetP1, P2…, pN be N points in the unit s-dimensional closed square Q = [0, 1]s. For any measurable set S ⊆ Q, we define δ(S), the discrepancy of S, by , where V(S) is the s-dimensional volume of S, and n(S), is the number of indices i for which pi∈S. Let 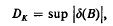, where the supermum is taken over all s-balls B ∈ Q, and 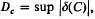, the supermum in this case being taken over all convex sets C ∈ Q. Clearly Dc ≧ Dk. In this paper we establish Theorem 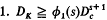, where φ1is a constant depending only on s.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 17 , Issue 1 , February 1974 , pp. 81 - 87
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Eggleston, H. G., Convexity, Cambridge Tract no. 47 (C. U. P. 1958).CrossRefGoogle Scholar
[2]Hlawka, E., ‘Zur Definitionen der Diskrepanz’, Acta Arith. 18 (1971), 233–241.CrossRefGoogle Scholar
[3]Smyth, C. J., Ph.D Dissertation, University of Cambridge, 1972.Google Scholar