Let 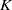$K$ be a commutative ring with unity, 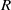$R$ an associative 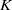$K$-algebra of characteristic different from 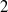$2$ with unity element and no nonzero nil right ideal, and 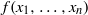$f({x}_{1} , \ldots , {x}_{n} )$ a multilinear polynomial over 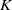$K$. Assume that, for all 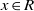$x\in R$ and for all 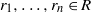${r}_{1} , \ldots , {r}_{n} \in R$ there exist integers 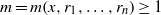$m= m(x, {r}_{1} , \ldots , {r}_{n} )\geq 1$ and 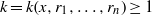$k= k(x, {r}_{1} , \ldots , {r}_{n} )\geq 1$ such that 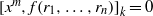$\mathop{[{x}^{m} , f({r}_{1} , \ldots , {r}_{n} )] }\nolimits_{k} = 0$. We prove that: (1) if 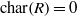$\text{char} (R)= 0$ then 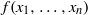$f({x}_{1} , \ldots , {x}_{n} )$ is central-valued on 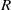$R$; and (2) if 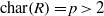$\text{char} (R)= p\gt 2$ and 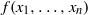$f({x}_{1} , \ldots , {x}_{n} )$ is not a polynomial identity in 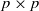$p\times p$ matrices of characteristic 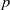$p$, then 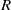$R$ satisfies 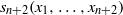${s}_{n+ 2} ({x}_{1} , \ldots , {x}_{n+ 2} )$ and for any 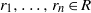${r}_{1} , \ldots , {r}_{n} \in R$ there exists 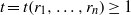$t= t({r}_{1} , \ldots , {r}_{n} )\geq 1$ such that 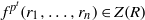${f}^{{p}^{t} } ({r}_{1} , \ldots , {r}_{n} )\in Z(R)$, the center of 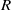$R$.