Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T00:21:45.305Z Has data issue: false hasContentIssue false
  • English
  • Français

HOMOGENEOUS AND H-CONTACT UNIT TANGENT SPHERE BUNDLES

Part of: Symplectic geometry, contact geometry Global differential geometry

Published online by Cambridge University Press:  12 May 2010

G. CALVARUSO  and
D. PERRONE
G. CALVARUSO
Affiliation:
Dipartimento di Matematica ‘E. De Giorgi’, Università del Salento, 73100 Lecce, Italy (email: [email protected])
D. PERRONE*
Affiliation:
Dipartimento di Matematica ‘E. De Giorgi’, Università del Salento, 73100 Lecce, Italy (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

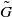We prove that all g-natural contact metric structures on a two-point homogeneous space are homogeneous contact. The converse is also proved for metrics of Kaluza–Klein type. We also show that if (M,g) is an Einstein manifold and is a Riemannian g-natural metric on T1M of Kaluza–Klein type, then 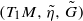is H-contact if and only if (M,g) is 2-stein, so proving that the main result of Chun et al. [‘H-contact unit tangent sphere bundles of Einstein manifolds’, Q. J. Math., to appear. DOI: 10.1093/qmath/hap025] is invariant under a two-parameter deformation of the standard contact metric structure on T1M. Moreover, we completely characterize Riemannian manifolds admitting two distinct H-contact g-natural contact metric structures, with associated metric of Kaluza–Klein type.

Keywords

two-point homogeneous spacesunit tangent sphere bundleg-natural metricH-contact spaces

MSC classification

Secondary: 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.) 53D10: Contact manifolds, general
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 88 , Issue 3 , June 2010 , pp. 323 - 337
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

Footnotes

The authors are supported by funds of the University of Salento and the MIUR (PRIN 2007).

References

[1]Abbassi, M. T. K.  and Calvaruso, G., ‘g-natural contact metrics on unit tangent sphere bundles’, Monatsh. Math. 151 (2006), 89–109.CrossRefGoogle Scholar
[2]Abbassi, M. T. K. and Calvaruso, G., ‘The curvature tensor of g-natural metrics on unit tangent sphere bundles’, Int. J. Contemp. Math. Sci. 3(6) (2008), 245–258.Google Scholar
[3]Abbassi, M. T. K. and Calvaruso, G., ‘Curvature properties of g-natural contact metric structures on unit tangent sphere bundles’, Beiträge Algebra Geom. 50(1) (2009), 155–178.Google Scholar
[4]Abbassi, M. T. K., Calvaruso, G. and Perrone, D., ‘Harmonic maps defined by the geodesic flow’, Houston J. Math. 36(1) (2010), 69–90.Google Scholar
[5]Abbassi, M. T. K. and Kowalski, O., ‘Naturality of homogeneous metrics on Stiefel manifolds SO(m+1)/SO(m−1)’, Differential Geom. Appl. 28 (2010), 131–139.CrossRefGoogle Scholar
[6]Abbassi, M. T. K. and Kowalski, O., ‘On Einstein Riemannian g-natural metrics on unit tangent sphere bundles’, submitted.Google Scholar
[7]Abbassi, M. T. K. and Sarih, M., ‘On some hereditary properties of Riemannian g-natural metrics on tangent bundles of Riemannian manifolds’, Differential Geom. Appl. 22(1) (2005), 19–47.CrossRefGoogle Scholar
[8]Benyounes, M., Loubeau, E. and Wood, C. M., ‘Harmonic maps and Kaluza–Klein metrics on spheres’, Arxiv:0809.2725v1.Google Scholar
[9]Blair, D. E., Riemannian Geometry of Contact and Symplectic Manifolds, Progress in Mathematics, 203 (Birkhäuser, Basel, 2002).CrossRefGoogle Scholar
[10]Boeckx, E., Perrone, D. and Vanhecke, L., ‘Unit tangent sphere bundles and two-point homogeneous spaces’, Period. Math. Hungar. 36 (1998), 79–95.CrossRefGoogle Scholar
[11]Boeckx, E. and Vanhecke, L., ‘Geometry of the unit tangent sphere bundle’ Public. Dep.to de Geometria y Topologia, Univ. Santiago de Compostela (Spain), 89 (1998), 5–17.Google Scholar
[12]Boeckx, E. and Vanhecke, L., ‘Harmonic and minimal vector fields on tangent and unit tangent bundles’, Differential Geom. Appl. 13 (2000), 77–93.CrossRefGoogle Scholar
[13]Calvaruso, G. and Perrone, D., ‘H-contact unit tangent sphere bundles’, Rocky Mountain J. Math. 37(5) (2007), 1419–1442.CrossRefGoogle Scholar
[14]Carpenter, P., Gray, A. and Willmore, T. J., ‘The curvature of Einstein symmetric spaces’, Q. J. Math. 33 (1982), 45–64.CrossRefGoogle Scholar
[15]Cheeger, J. and Gromoll, D., ‘On the structure of complete manifolds of nonnegative curvature’, Ann. of Math. (2) 96 (1972), 413–443.CrossRefGoogle Scholar
[16]Chi, Q. S., ‘A curvature characterization of certain locally rank-one symmetric spaces’, J. Differential Geom. 28 (1988), 187–202.Google Scholar
[17]Chun, S. H., Park, J. H. and Sekigawa, K., ‘H-contact unit tangent sphere bundles of Einstein manifolds’, Q. J. Math., to appear. DOI: 10.1093/qmath/hap025.CrossRefGoogle Scholar
[18]Koufogiorgos, T., Markellos, M. and Papantoniou, V. J., ‘The harmonicity of the Reeb vector field on contact metric three-manifolds’, Pacific J. Math. 234(2) (2008), 325–344.CrossRefGoogle Scholar
[19]Kowalski, O. and Sekizawa, M., ‘Invariance of g-natural metrics on tangent bundles’, Differential Geom. Appl., 171–181 (World Sci. Publ., Hackensack, NJ, 2008).CrossRefGoogle Scholar
[20]Musso, E. and Tricerri, F., ‘Riemannian metrics on tangent bundles’, Ann. Mat. Pura Appl. 150(4) (1988), 1–20.CrossRefGoogle Scholar
[21]Nikolayevsky, Y., ‘Osserman manifolds of dimension 8’, Manuscripta Math. 115 (2004), 31–53.CrossRefGoogle Scholar
[22]Nikolayevsky, Y., ‘Osserman conjecture in dimension n≠8,16’, Math. Ann. 331 (2005), 505–522.CrossRefGoogle Scholar
[23]Perrone, D., ‘Harmonic characteristic vector fields on contact metric three manifolds’, Bull. Aust. Math. Soc. 67 (2003), 305–315.CrossRefGoogle Scholar
[24]Perrone, D., ‘Contact metric manifolds whose characteristic vector field is a harmonic vector field’, Differential Geom. Appl. 20 (2004), 367–378.CrossRefGoogle Scholar
[25]Wolf, J. A., Spaces of Constant Curvature (McGraw-Hill, New York, 1967).Google Scholar
[26]Wood, C. M., ‘An existence theorem for harmonic sections’, Manuscripta Math. 68 (1990), 69–75.CrossRefGoogle Scholar