Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T04:01:39.791Z Has data issue: false hasContentIssue false
  • English
  • Français

HOLOMORPHIC FUNCTIONS WITH IMAGE OF GIVEN LOGARITHMIC OR ELLIPTIC CAPACITY

Part of: Geometric function theory Two-dimensional theory

Published online by Cambridge University Press:  08 March 2013

DIMITRIOS BETSAKOS
DIMITRIOS BETSAKOS*
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For holomorphic functions 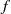$f$ in the unit disk 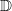$ \mathbb{D} $ with 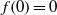$f(0)= 0$, we prove a modulus growth bound involving the logarithmic capacity (transfinite diameter) of the image. We show that the pertinent extremal functions map the unit disk conformally onto the interior of an ellipse. We prove a modulus growth bound for elliptically schlicht functions in terms of the elliptic capacity 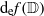${\mathrm{d} }_{\mathrm{e} } f( \mathbb{D} )$ of the image. We also show that the function 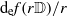${\mathrm{d} }_{\mathrm{e} } f(r \mathbb{D} )/ r$ is increasing for 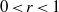$0\lt r\lt 1$.

Keywords

holomorphic functionlogarithmic capacityelliptic capacitycondenser capacityelliptically schlicht functionSchwarz’s lemmasymmetrizationextremal length

MSC classification

Secondary: 30C80: Maximum principle; Schwarz's lemma, Lindelöf principle, analogues and generalizations; subordination 30C85: Capacity and harmonic measure in the complex plane 31A15: Potentials and capacity, harmonic measure, extremal length
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 2 , April 2013 , pp. 145 - 157
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Anderson, G. D., Vamanamurthy, M. K. and Vuorinen, M., Conformal Invariants, Inequalities, and Quasiconformal Maps (Wiley, New York, 1997).Google Scholar
Betsakos, D., ‘Elliptic, hyperbolic, and condenser capacity; geometric estimates for elliptic capacity’, J. Anal. Math. 96 (2005), 37–55.CrossRefGoogle Scholar
Burckel, R. B., Marshall, D. E., Minda, D., Poggi-Corradini, P. and Ransford, T. J., ‘Area, capacity and diameter versions of Schwarz’s lemma’, Conform. Geom. Dyn. 12 (2008), 133–152.CrossRefGoogle Scholar
Cunningham, R., ‘Univalent functions of given transfinite diameter: a maximum modulus problem’, Ann. Acad. Sci. Fenn. Math. 18 (1993), 249–271.Google Scholar
Dubinin, V. N., ‘Symmetrization in the geometric theory of functions of a complex variable’, Uspekhi Mat. Nauk 49 (1994), 3–76 (in Russian); translation in Russian Math. Surveys 49 (1994), 1–79.Google Scholar
Duren, P. and Kühnau, R., ‘Elliptic capacity and its distortion under conformal mapping’, J. Anal. Math. 89 (2003), 317–335.CrossRefGoogle Scholar
Garnett, J. B. and Marshall, D. E., Harmonic Measure (Cambridge University Press, Cambridge, 2005).CrossRefGoogle Scholar
Hayman, W. K., Multivalent Functions, 2nd edn (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar
Jenkins, J. A., Univalent Functions and Conformal Mapping (Springer, Berlin, 1958).Google Scholar
Kraus, D. and Roth, O., ‘Weighted distortion in conformal mapping in Euclidean, hyperbolic and elliptic geometry’, Ann. Acad. Sci. Fenn. Math. 31 (2006), 111–130.Google Scholar
Kühnau, R., ‘Über vier Klassen schlichter Funkionen’, Math. Nachr. 50 (1971), 17–26.CrossRefGoogle Scholar
Kühnau, R., ‘Variation of diametrically symmetric or elliptically schlicht conformal mappings’, J. Anal. Math. 89 (2003), 303–316.CrossRefGoogle Scholar
Pouliasis, S., ‘Condenser capacity and meromorphic functions’, Comput. Methods Funct. Theory 11 (2011), 237–245.CrossRefGoogle Scholar
Ransford, T., Potential Theory in the Complex Plane (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Remmert, R., Classical Topics in Complex Function Theory (Springer, New York, 1998).CrossRefGoogle Scholar
Schippers, E. D., ‘Estimates on kernel functions of elliptically schlicht domains’, Comput. Methods Funct. Theory 2 (2002), 579–596.CrossRefGoogle Scholar
Shah, T.-S., ‘On the moduli of some classes of analytic functions’, Acta Math. Sinica 5 (1955), 439–454 (in Chinese. English summary).Google Scholar