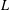Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T10:39:40.206Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER ORDER CONGRUENCES AMONGST HASSE–WEIL $L$-VALUES

Part of: Whitehead groups and $K_1$ Arithmetic algebraic geometry Algebraic number theory: global fields

Published online by Cambridge University Press:  14 October 2014

DANIEL DELBOURGO  and
LLOYD PETERS
DANIEL DELBOURGO*
Affiliation:
Department of Mathematics, University of Waikato, Hamilton 3240, New Zealand email [email protected]
LLOYD PETERS
Affiliation:
School of Mathematical Sciences, Monash University, Melbourne 3800, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the 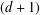$(d+1)$-dimensional Lie group 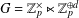$G=\mathbb{Z}_{p}^{\times }\ltimes \mathbb{Z}_{p}^{\oplus d}$, we determine through the use of 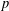$p$-power congruences a necessary and sufficient set of conditions whereby a collection of abelian 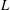$L$-functions arises from an element in 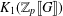$K_{1}(\mathbb{Z}_{p}\unicode[STIX]{x27E6}G\unicode[STIX]{x27E7})$. If 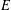$E$ is a semistable elliptic curve over 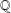$\mathbb{Q}$, these abelian 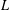$L$-functions already exist; therefore, one can obtain many new families of higher order 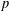$p$-adic congruences. The first layer congruences are then verified computationally in a variety of cases.

Keywords

Iwasawa theoryelliptic curvesK-theoryL-functions

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 19B28: $K_1$ of group rings and orders
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 1 , February 2015 , pp. 1 - 38
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bouganis, A., ‘Special values of L-functions and false Tate curve extensions’, J. Lond. Math. Soc. (2) 82 (2010), 596–620.CrossRefGoogle Scholar
Bouganis, A. and Dokchitser, V., ‘Algebraicity of L-values for elliptic curves in a false Tate curve tower’, Math. Proc. Cambridge Philos. Soc. 142 (2007), 193–204.Google Scholar
Burns, D. and Venjakob, O., ‘On descent theory and main conjectures in noncommutative Iwasawa theory’, J. Inst. Math. Jussieu 142 (2011), 59–118.Google Scholar
Coates, J., Schneider, P., Sujatha, R. and Venjakob, O. (eds) ‘Noncommutative Iwasawa main conjectures over totally real fields’, in: Proc. Münster Workshop on Iwasawa Theory, Springer Proceedings in Mathematics and Statistics, 29 (Springer, Berlin, Heidelberg, 2013).Google Scholar
Delbourgo, D. and Lei, A., ‘Noncommutative Iwasawa theory for elliptic curves with multiplicative reduction’, Preprint, 2014.Google Scholar
Delbourgo, D. and Ward, T., ‘Nonabelian congruences between L-values of elliptic curves’, Ann. Inst. Fourier (Grenoble) 58 (2008), 1023–1055.Google Scholar
Delbourgo, D. and Ward, T., ‘The growth of CM periods over false Tate extensions’, Exp. Math. 19 (2010), 195–210.Google Scholar
Dokchitser, V. and Dokchitser, T., ‘Computations in noncommutative Iwasawa theory’, Proc. Lond. Math. Soc. (3) 94 (2007), 211–272.CrossRefGoogle Scholar
Hara, T., ‘Iwasawa theory of totally real fields for certain noncommutative p-extensions’, J. Number Theory 130 (2010), 1068–1097.Google Scholar
Kakde, M., ‘The main conjecture of Iwasawa theory for totally real fields’, Invent. Math. 193 (2013), 539–626.CrossRefGoogle Scholar
Kato, K., ‘K 1of some noncommutative completed group rings’, J. K-Theory 34 (2005), 99–140.Google Scholar
Kato, K., ‘Iwasawa theory of totally real fields for Galois extensions of Heisenberg type’, Preprint.Google Scholar
Kato, K., Sujatha, R., Venjakob, O., Coates, J. and Fukaya, T., ‘The G L 2main conjecture for elliptic curves without complex multiplication’, Publ. Math. Inst. Hautes Études Sci. 101 (2005), 163–208.Google Scholar
Oliver, R., Whitehead Groups of Finite Groups, LMS Lecture Note Series, 132 (Cambridge University Press, London, 1988).CrossRefGoogle Scholar
Peters, L., ‘Noncommutative Iwasawa theory for $d$-fold false Tate extensions’, PhD Thesis, Monash University, 2014.Google Scholar
Ritter, J. and Weiss, A., ‘Toward equivariant Iwasawa theory. III’, Math. Ann. 336 (2006), 27–49.Google Scholar
Serre, J.-P., Linear Representations of Finite Groups, Graduate Texts in Mathematics, 42 (Springer, New York, 1977).CrossRefGoogle Scholar