Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T19:18:25.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic analysis for groups acting on triangle buildings

Part of: Abstract harmonic analysis Lie groups Finite geometry and special incidence structures

Published online by Cambridge University Press:  09 April 2009

Donald I. Cartwright  and
Wojciech MŁotkowski
Donald I. Cartwright
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW 2006, Australia
Wojciech MŁotkowski
Affiliation:
Institute of Mathematics, The University of Wrocław, pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

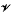Let Δ be a thick building of type Ã2, and let be its set of vertices. We study a commutative algebra 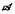of ‘averaging’ operators acting on the space of complex valued functions on 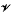. This algebra may be identified with a space of ‘biradial functions’ on 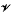, or with a convolution algebra of bi-K-invariant functions on G, if G is a sufficiently large group of ‘type-rotating’ automorphisms of Δ, and K is the subgroup of G fixing a given vertex. We describe the multiplicative functionals on 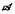and the corresponding spherical functions. We consider the C*-algebra induced by 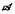on l2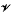, find its spectrum Σ, prove positive definiteness of a kernel kz for each z ∈ Σ, find explicity the spherical Plancherel formula for any group G of type rotating automorphisms, and discuss the irreducibility of the unitary representations appearing therein. For the class of buildings ΔJ arising from the groups ΓJ introduced in [2], this involves proving that the weak closure of 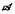is maximal abelian in the von Neumann algebra generated by the left regular representation of ΓJ.

Keywords

triangle buildingsspherical Plancherel formula.

MSC classification

Secondary: 51E24: Buildings and the geometry of diagrams 22E50: Representations of Lie and linear algebraic groups over local fields 43A35: Positive definite functions on groups, semigroups, etc. 43A90: Spherical functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 56 , Issue 3 , June 1994 , pp. 345 - 383
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Brown, K. S., Buildings (Springer, New York, 1989).CrossRefGoogle Scholar
[2]Cartwright, D. I., Mantero, A. M., Steger, T. and Zappa, A., ‘Groups acting simply transitively on the vertices of a building of type Ã2 I’, Geom. Ded. 47 (1993), 143–166.CrossRefGoogle Scholar
[3]Cartwright, D. I., Mantero, A. M., Steger, T. and Zappa, A., ‘Groups acting simply transitively on the vertices of a building of type Ã2 II: the cases q = 2 and q = 3’, Geom. Ded. 47 (1993), 167–223.CrossRefGoogle Scholar
[4]Cowling, M. G. and Steger, T., ‘The irreducibility of restrictions of unitary representations to lattices’, J. Reine Angew. Math. 420 (1991), 85–98.Google Scholar
[5]Figà-Talamanca, A. and Nebbia, C., Harmonic analysis and representation theory for groups acting on homogeneous trees, London Math. Soc. Lecture Note Ser. 162 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
[6]Figà-Talamanca, A. and Picardello, M. A., Harmonic analysis on free groups, Lect. Notes Pure Appl. Math. 87 (Marcel Dekker, New York, 1983).Google Scholar
[7]Macdonald, I. G., Spherical functions on a group of p-adic type, Ramanujan Inst. Publications 2 (University of Madras, 1971).Google Scholar
[8]Pedersen, G. K., Analysis now, Graduate Texts in Math. 118 (Springer, New York, 1989).CrossRefGoogle Scholar
[9]Pytlik, T., ‘Radial functions on free groups and a decomposition of the regular representation into irreducible components’, J. Reine Angew. Math. 326 (1981), 124–135.Google Scholar
[10]Ronan, M., Lectures on Buildings, Perspect. in Math. 7 (Academic Press, New York, 1989).Google Scholar
[11]Serre, J-P., Trees (Springer-Verlag, New York, 1980).CrossRefGoogle Scholar
[12]Tits, J., ‘Spheres of radius 2 in triangle buildings. I’, in: Finite geometries, buildings, and related topics (eds. Kantor, W. et al. ) (Clarendon Press, Oxford, 1990) pp. 17–28.CrossRefGoogle Scholar