Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T13:43:42.418Z Has data issue: false hasContentIssue false
  • English
  • Français

HARDY’S THEOREM FOR GABOR TRANSFORM

Part of: Locally compact groups and their algebras Abstract harmonic analysis Lie groups

Published online by Cambridge University Press:  15 August 2018

ASHISH BANSAL Open the ORCID record for ASHISH BANSAL [Opens in a new window] ,
AJAY KUMAR Open the ORCID record for AJAY KUMAR [Opens in a new window]  and
JYOTI SHARMA
ASHISH BANSAL
Affiliation:
Department of Mathematics, Keshav Mahavidyalaya (University of Delhi), H-4-5 Zone, Pitampura, Delhi-110034, India email [email protected]
AJAY KUMAR*
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India email [email protected]
JYOTI SHARMA
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Hardy’s uncertainty principle for the Gabor transform is proved for locally compact abelian groups having noncompact identity component and groups of the form 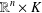$\mathbb{R}^{n}\times K$, where 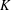$K$ is a compact group having irreducible representations of bounded dimension. We also show that Hardy’s theorem fails for a connected nilpotent Lie group 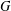$G$ which admits a square integrable irreducible representation. Further, a similar conclusion is made for groups of the form 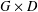$G\times D$, where 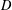$D$ is a discrete group.

Keywords

Hardy’s theoremFourier transformcontinuous Gabor transformnilpotent Lie group

MSC classification

Primary: 43A32: Other transforms and operators of Fourier type
Secondary: 22D99: None of the above, but in this section 22E25: Nilpotent and solvable Lie groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 2 , April 2019 , pp. 143 - 159
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The last author is supported by UGC under joint UGC-CSIR Junior Research Fellowship (Ref. No. 21/12/2014(ii)EU-V).

References

Baklouti, A. and Kaniuth, E., ‘On Hardy’s uncertainty principle for connected nilpotent Lie groups’, Math. Z. 259(2) (2008), 233–247.Google Scholar
Baklouti, A. and Kaniuth, E., ‘On Hardy’s uncertainty principle for solvable locally compact groups’, J. Fourier Anal. Appl. 16(1) (2010), 129–147.Google Scholar
Corwin, L. and Greenleaf, F. P., Representations of Nilpotent Lie Groups and Their Applications, Part I. Basic Theory and Examples (Cambridge University Press, Cambridge, 1990).Google Scholar
Farashahi, A. G. and Kamyabi-Gol, R., ‘Continuous Gabor transform for a class of non-abelian groups’, Bull. Belg. Math. Soc. Simon Stevin 19 (2012), 683–701.Google Scholar
Folland, G. B., ‘The uncertainty principle: a mathematical survey’, J. Fourier Anal. Appl. 3(3) (1997), 207–238.Google Scholar
Gröchenig, K., ‘Uncertainty principles for time–frequency representations’, in: Advances in Gabor Analysis, Applied and Numerical Harmonic Analysis (Birkhäuser, Boston, MA, 2003), 11–30.Google Scholar
Hardy, G. H., ‘A theorem concerning Fourier transforms’, J. Lond. Math. Soc. 1(3) (1933), 227–231.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vols I and II (Springer-Verlag, Berlin, 1963 and 1970).Google Scholar
Kaniuth, E. and Kumar, A., ‘Hardy’s theorem for simply connected nilpotent Lie groups’, Math. Proc. Cambridge Philos. Soc. 131(3) (2001), 487–494.Google Scholar
Moore, C. C., ‘Groups with finite dimensional irreducible representation’, Trans. Amer. Math. Soc. 166 (1972), 401–410.Google Scholar
Nielson, O. A., Unitary Representations and Coadjoint Orbits of Low-dimensional Nilpotent Lie Groups, Queen’s Papers in Pure and Applied Mathematics (Queen’s University, Kingston, ON, 1983).Google Scholar
Parui, S. and Thangavelu, S., ‘On theorems of Beurling and Hardy for certain step two nilpotent groups’, Integral Transforms Spec. Funct. 20(2) (2009), 127–145.Google Scholar
Ray, S. K., ‘Uncertainty principles on two step nilpotent Lie groups’, Proc. Indian Acad. Sci. Math. Sci. 111(3) (2001), 293–318.Google Scholar
Sarkar, R. P. and Thangavelu, S., ‘A complete analogue of Hardy’s theorem on semisimple Lie groups’, Colloq. Math. 93(1) (2002), 27–40.Google Scholar
Sarkar, R. P. and Thangavelu, S., ‘On theorems of Beurling and Hardy for the Euclidean motion group’, Tohoku Math. J. 57(3) (2005), 335–351.Google Scholar
Sitaram, A., Sundari, M. and Thangavelu, S., ‘Uncertainty principles on certain Lie groups’, Proc. Indian Acad. Sci. Math. Sci. 105(2) (1995), 135–151.Google Scholar
Sundari, M., ‘Hardy’s theorem for the n-dimensional Euclidean motion group’, Proc. Amer. Math. Soc. 126(4) (1998), 1199–1204.Google Scholar
Thangavelu, S., ‘An analogue of Hardy’s theorem for the Heisenberg group’, Colloq. Math. 87(1) (2001), 137–145.Google Scholar