Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T17:32:04.206Z Has data issue: false hasContentIssue false
  • English
  • Français

HARDY SPACES ON METRIC MEASURE SPACES WITH GENERALIZED SUB-GAUSSIAN HEAT KERNEL ESTIMATES

Part of: Harmonic analysis in several variables Partial differential equations on manifolds; differential operators Elliptic equations and systems

Published online by Cambridge University Press:  14 August 2017

LI CHEN
LI CHEN*
Affiliation:
Instituto de Ciencias Matemáticas CSIC-UAM-UC3M-UCM, Consejo Superior de Investigaciones Científicas, C/ Nicolás Cabrera, 13–15, E-28049 Madrid, Spain email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Hardy space theory has been studied on manifolds or metric measure spaces equipped with either Gaussian or sub-Gaussian heat kernel behaviour. However, there are natural examples where one finds a mix of both behaviours (locally Gaussian and at infinity sub-Gaussian), in which case the previous theory does not apply. Still we define molecular and square function Hardy spaces using appropriate scaling, and we show that they agree with Lebesgue spaces in some range. Besides, counterexamples are given in this setting that the 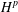$H^{p}$ space corresponding to Gaussian estimates may not coincide with 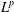$L^{p}$ . As a motivation for this theory, we show that the Riesz transform maps our Hardy space 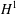$H^{1}$ into 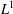$L^{1}$ .

Keywords

Hardy spacesmetric measure spacesheat kernel estimatesRiesz transforms

MSC classification

Primary: 42B35: Function spaces arising in harmonic analysis
Secondary: 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation 58J35: Heat and other parabolic equation methods 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 2 , April 2018 , pp. 162 - 194
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Amenta, A., ‘Tent spaces over metric measure spaces under doubling and related assumptions’, in: Operator Theory in Harmonic and Non-Commutative Analysis, Operator Theory: Advances and Applications, 240 (Birkhäuser/Springer, Cham, 2014), 1–29.Google Scholar
Auscher, P., ‘On necessary and sufficient conditions for L p -estimates of Riesz transforms associated to elliptic operators on ℝ n and related estimates’, Mem. Amer. Math. Soc. 186(871) (2007), xviii+75.Google Scholar
Auscher, P., Hofmann, S. and Martell, J.-M., ‘Vertical versus conical square functions’, Trans. Amer. Math. Soc. 364(10) (2012), 5469–5489.CrossRefGoogle Scholar
Auscher, P., McIntosh, A. and Morris, A., ‘Calderón reproducing formulas and applications to Hardy spaces’, Rev. Mat. Iberoam. 31(3) (2015), 865–900.Google Scholar
Auscher, P., McIntosh, A. and Russ, E., ‘Hardy spaces of differential forms on Riemannian manifolds’, J. Geom. Anal. 18(1) (2008), 192–248.CrossRefGoogle Scholar
Bakry, D. and Émery, M., ‘Diffusions hypercontractives’, in: Séminaire de probabilités, XIX, 1983/84, Lecture Notes in Mathematics, 1123 (Springer, Berlin, 1985), 177–206.Google Scholar
Barlow, M. T., ‘Which values of the volume growth and escape time exponent are possible for a graph?’, Rev. Mat. Iberoam. 20(1) (2004), 1–31.CrossRefGoogle Scholar
Barlow, M. T., ‘Analysis on the Sierpinski carpet’, in: Analysis and Geometry of Metric Measure Spaces, CRM Proceedings and Lecture Notes, 56 (American Mathematical Society, Providence, RI, 2013), 27–53.Google Scholar
Barlow, M. T. and Bass, R. F., ‘Stability of parabolic Harnack inequalities’, Trans. Amer. Math. Soc. 356(4) (2004), 1501–1533.Google Scholar
Barlow, M. T., Coulhon, T. and Grigor’yan, A., ‘Manifolds and graphs with slow heat kernel decay’, Invent. Math. 144(3) (2001), 609–649.CrossRefGoogle Scholar
Bergh, J. and Löfström, J., Interpolation Spaces. An Introduction, Grundlehren der mathematischen Wissenschaften, 223 (Springer, Berlin, 1976).Google Scholar
Blunck, S., ‘Generalized Gaussian estimates and Riesz means of Schrödinger groups’, J. Aust. Math. Soc. 82(2) (2007), 149–162.Google Scholar
Blunck, S. and Kunstmann, P. C., ‘Generalized Gaussian estimates and the legendre transform’, J. Operator Theory 53(2) (2005), 351–365.Google Scholar
Chen, L., Coulhon, T., Feneuil, J. and Russ, E., ‘Riesz transform for 1 ≤ p ≤ 2 without Gaussian heat kernel bound’, J. Geom. Anal. 27(2) (2017), 1489–1514.CrossRefGoogle Scholar
Chen, P., Duong, X. T., Li, J., Ward, L. A. and Yan, L. X., ‘Product Hardy spaces associated to operators with heat kernel bounds on spaces of homogeneous type’, Math. Z. 282 (2016), 1033–1065.CrossRefGoogle Scholar
Coifman, R. R., Meyer, Y. and Stein, E. M., ‘Some new function spaces and their applications to harmonic analysis’, J. Funct. Anal. 62(2) (1985), 304–335.CrossRefGoogle Scholar
Coifman, R. R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes, Lecture Notes in Mathematics, 242 (Springer, Berlin, 1971).Google Scholar
Coifman, R. R. and Weiss, G., ‘Extensions of Hardy spaces and their use in analysis’, Bull. Amer. Math. Soc. 83(4) (1977), 569–645.CrossRefGoogle Scholar
Coulhon, T., ‘Dimension à l’infini d’un semi-groupe analytique’, Bull. Sci. Math. 114(4) (1990), 485–500.Google Scholar
Coulhon, T. and Sikora, A., ‘Gaussian heat kernel upper bounds via the Phragmén–Lindelöf theorem’, Proc. Lond. Math. Soc. (3) 96(2) (2008), 507–544.Google Scholar
Cowling, M., Doust, I., McIntosh, A. and Yagi, A., ‘Banach space operators with a bounded H ∞ functional calculus’, J. Aust. Math. Soc. Ser. A 60(1) (1996), 51–89.Google Scholar
Duong, X. T. and McIntosh, A., ‘Singular integral operators with non-smooth kernels on irregular domains’, Rev. Mat. Iberoam. 15(2) (1999), 233–265.Google Scholar
Fefferman, C. and Stein, E. M., ‘ H p spaces of several variables’, Acta Math. 129(3–4) (1972), 137–193.Google Scholar
Feneuil, J., ‘Riesz transform on graphs under subgaussian estimates’, Preprint, 2015, arXiv:1505.07001.Google Scholar
Feneuil, J., ‘Hardy and BMO spaces on graphs, application to Riesz transform’, Potential Anal. 45(1) (2016), 1–54.Google Scholar
Grafakos, L., Classical Fourier Analysis, Graduate Texts in Mathematics, 249 (Springer, New York, 2008).Google Scholar
Grigor’yan, A., Heat Kernel and Analysis on Manifolds, AMS/IP Studies in Advanced Mathematics, 47 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Gyrya, P. and Saloff-Coste, L., ‘Neumann and Dirichlet heat kernels in inner uniform domains’, Astérisque 336 (2011), viii+144.Google Scholar
Hebisch, W. and Saloff-Coste, L., ‘On the relation between elliptic and parabolic Harnack inequalities’, Ann. Inst. Fourier (Grenoble) 51(5) (2001), 1437–1481.CrossRefGoogle Scholar
Hofmann, S., Lu, G., Mitrea, D., Mitrea, M. and Yan, L., ‘Hardy spaces associated to non-negative self-adjoint operators satisfying Davies–Gaffney estimates’, Mem. Amer. Math. Soc. 214(1007) (2011), vi+78.Google Scholar
Hofmann, S. and Martell, J. M., ‘ L p bounds for Riesz transforms and square roots associated to second order elliptic operators’, Publ. Mat. 47(2) (2003), 497–515.Google Scholar
Hofmann, S. and Mayboroda, S., ‘Hardy and BMO spaces associated to divergence form elliptic operators’, Math. Ann. 344(1) (2009), 37–116.Google Scholar
Kunstmann, P. C. and Uhl, M., ‘Spectral multiplier theorems of Hörmander type on Hardy and Lebesgue spaces’, J. Operator Theory 73(1) (2015), 27–69.Google Scholar
Li, P., Geometric Analysis, Cambridge Studies in Advanced Mathematics, 134 (Cambridge University Press, Cambridge, 2012).Google Scholar
Russ, E., ‘The atomic decomposition for tent spaces on spaces of homogeneous type’, in: CMA/AMSI Research Symposium ‘Asymptotic Geometric Analysis, Harmonic Analysis, and Related Topics’, Proceedings of the Centre for Mathematics and its Applications, Australian National University, 42 (Australian National University, Canberra, 2007), 125–135.Google Scholar
Stein, E. M., Topics in Harmonic Analysis Related to the Littlewood–Paley Theory, Annals of Mathematics Studies, 63 (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series, 43 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Sturm, K.-T., ‘Analysis on local Dirichlet spaces. I. Recurrence, conservativeness and L p -Liouville properties’, J. reine angew. Math. 456 (1994), 173–196.Google Scholar
Sturm, K.-T., ‘Analysis on local Dirichlet spaces. II. Upper Gaussian estimates for the fundamental solutions of parabolic equations’, Osaka J. Math. 32(2) (1995), 275–312.Google Scholar
Uhl, M., ‘Spectral multiplier theorems of Hörmander type via generalized Gaussian estimates’, PhD Thesis, Karlsruher Institut für Technologie (KIT), 2011.Google Scholar
Varopoulos, N. Th., ‘Long range estimates for Markov chains’, Bull. Sci. Math. (2) 109(3) (1985), 225–252.Google Scholar