Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T09:57:22.488Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUP ALGEBRAS WITH ENGEL UNIT GROUPS

Part of: Rings and algebras arising under various constructions Rings with polynomial identity Representation theory of groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  16 March 2016

M. RAMEZAN-NASSAB
M. RAMEZAN-NASSAB*
Affiliation:
Department of Mathematics, Kharazmi University, 50 Taleghani St., Tehran, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 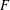$F$ be a field of characteristic 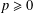$p\geq 0$ and 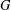$G$ any group. In this article, the Engel property of the group of units of the group algebra 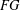$FG$ is investigated. We show that if 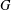$G$ is locally finite, then 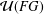${\mathcal{U}}(FG)$ is an Engel group if and only if 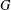$G$ is locally nilpotent and 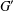$G^{\prime }$ is a 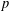$p$-group. Suppose that the set of nilpotent elements of 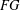$FG$ is finite. It is also shown that if 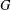$G$ is torsion, then 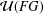${\mathcal{U}}(FG)$ is an Engel group if and only if 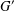$G^{\prime }$ is a finite 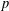$p$-group and 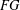$FG$ is Lie Engel, if and only if 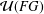${\mathcal{U}}(FG)$ is locally nilpotent. If 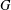$G$ is nontorsion but 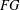$FG$ is semiprime, we show that the Engel property of 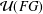${\mathcal{U}}(FG)$ implies that the set of torsion elements of 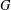$G$ forms an abelian normal subgroup of 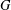$G$.

Keywords

group algebraEngel groupLie Engel ring

MSC classification

Primary: 16R50: Other kinds of identities (generalized polynomial, rational, involution)
Secondary: 16S34: Group rings , Laurent polynomial rings 20C07: Group rings of infinite groups and their modules 20F45: Engel conditions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 2 , October 2016 , pp. 244 - 252
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Bovdi, A., ‘Group algebras with an Engel group of units’, J. Aust. Math. Soc. 80 (2006), 173–178.Google Scholar
Bovdi, A. and Khripta, I. I., ‘The Engel property of the multiplicative group of a group algebra’, Mat. Sb. 182 (1991), 130–144 (in Russian); English translation in Math. USSR Sb. 72 (1992), 121–134.Google Scholar
Giambruno, A., Jespers, E. and Valenti, A., ‘Group identities on units of rings’, Arch. Math. 63 (1994), 291–296.Google Scholar
Giambruno, A., Sehgal, S. K. and Valenti, A., ‘Group algebras whose units satisfy a group identity’, Proc. Amer. Math. Soc. 125 (1997), 629–634.Google Scholar
Giambruno, A., Sehgal, S. K. and Valenti, A., ‘Group identities on units of group algebras’, J. Algebra 226 (2000), 488–504.Google Scholar
Lee, G. T., Group Identities on Units and Symmetric Units of Group Rings, Algebra and Applications, 12 (Springer, London, 2010).CrossRefGoogle Scholar
Liu, C.-H., ‘Group algebras with units satisfying a group identity’, Proc. Amer. Math. Soc. 127 (1999), 327–336.CrossRefGoogle Scholar
Liu, C.-H. and Passman, D. S., ‘Group algebras with units satisfying a group identity II’, Proc. Amer. Math. Soc. 127 (1999), 337–341.Google Scholar
Passman, D. S., The Algebraic Structure of Group Rings (Wiley, New York, 1977).Google Scholar
Ramezan-Nassab, M., ‘Group algebras with locally nilpotent unit groups’, Comm. Algebra 44 (2016), 604–612.CrossRefGoogle Scholar
Ramezan-Nassab, M. and Kiani, D., ‘Some skew linear groups with Engel’s condition’, J. Group Theory 15 (2012), 529–541.Google Scholar
Ramezan-Nassab, M. and Kiani, D., ‘Rings satisfying generalized Engel conditions’, J. Algebra Appl. 11 1250121 (2012), 8 pages.CrossRefGoogle Scholar
Riley, D. M., ‘Group algebras with units satisfying an Engel identity’, Rend. Circ. Mat. Palermo (2) 49 (2000), 540–544.CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups, 2nd edn (Springer, New York, 1996).Google Scholar
Sehgal, S. K., Topics in Group Rings (Marcel Dekker, New York, 1978).Google Scholar
Shalev, A., ‘On associative algebras satisfying the Engel condition’, Israel J. Math. 67 (1989), 287–290.Google Scholar