Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Guangbing
and
Tang, X.H.
2014.
Nehari-type ground state solutions for Schrödinger equations including critical exponent.
Applied Mathematics Letters,
Vol. 37,
Issue. ,
p.
101.
Liu, Hongliang
and
Chen, Haibo
2015.
Ground-state solution for a class of biharmonic equations including critical exponent.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 66,
Issue. 6,
p.
3333.
Liu, Hongliang
and
Chen, Haibo
2015.
Least energy nodal solution for quasilinear biharmonic equations with critical exponent inRN.
Applied Mathematics Letters,
Vol. 48,
Issue. ,
p.
85.
Khoutir, Sofiane
and
Chen, Haibo
2017.
Ground state solutions and least energy sign-changing solutions for a class of fourth order Kirchhoff-type equations in <mml:math altimg="si1.gif" display="inline" overflow="scroll" xmlns:xocs="http://www.elsevier.com/xml/xocs/dtd" xmlns:xs="http://www.w3.org/2001/XMLSchema" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns="http://www.elsevier.com/xml/ja/dtd" xmlns:ja="http://www.elsevier.com/xml/ja/dtd" xmlns:mml="http://www.w3.org/1998/Math/MathML" xmlns:tb="http://www.elsevier.com/xml/common/table/dtd" xmlns:sb="http://www.elsevier.com/xml/common/struct-bib/dtd" xmlns:ce="http://www.elsevier.com/xml/common/dtd" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:cals="http://www.elsevier.com/xml/common/cals/dtd" xmlns:sa="http://www.elsevier.com/xml/common/struct-aff/dtd"><mml:msup><mml:mrow><mml:mi mathvariant="double-struck">R</mml:mi></mml:mrow><mml:mrow><mml:mi>N</mml:mi></mml:mrow></mml:msup></mml:math>.
Arab Journal of Mathematical Sciences,
Vol. 23,
Issue. 1,
p.
94.
Che, Guofeng
and
Chen, Haibo
2017.
Nontrivial solutions and least energy nodal solutions for a class of fourth-order elliptic equations.
Journal of Applied Mathematics and Computing,
Vol. 53,
Issue. 1-2,
p.
33.
Khoutir, Sofiane
and
Chen, Haibo
2017.
Least energy sign-changing solutions for a class of fourth order Kirchhoff-type equations in $$\mathbb {R}^{N}$$ R N.
Journal of Applied Mathematics and Computing,
Vol. 55,
Issue. 1-2,
p.
25.
Chen, Yi
and
Tang, Xianhua
2020.
Nehari-type ground state solutions for Schrödinger equations with Hardy potential and critical nonlinearities.
Complex Variables and Elliptic Equations,
Vol. 65,
Issue. 8,
p.
1315.
刘, 文静
2023.
Existence of Ground State Solutions for a Class of p-Laplace Equations.
Advances in Applied Mathematics,
Vol. 12,
Issue. 01,
p.
411.
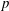 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-SUPERLINEAR
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-SUPERLINEAR 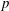 $p$-LAPLACIAN EQUATIONS
$p$-LAPLACIAN EQUATIONS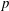 $p$-Laplacian equation which weaken the Ambrosetti–Rabinowitz type condition and the monotonicity condition for the function
$p$-Laplacian equation which weaken the Ambrosetti–Rabinowitz type condition and the monotonicity condition for the function 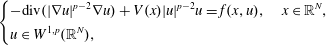 $$\begin{equation*} \left \{ \begin{array}{@{}ll} -\mathrm {div}(|\nabla u|^{p-2}\nabla u)+V(x)|u|^{p-2}u=f(x, u), \quad x\in {\mathbb {R}}^{N},\\[5pt] u\in W^{1, p}({\mathbb {R}}^{N}), \end{array} \right . \end{equation*}$$
$$\begin{equation*} \left \{ \begin{array}{@{}ll} -\mathrm {div}(|\nabla u|^{p-2}\nabla u)+V(x)|u|^{p-2}u=f(x, u), \quad x\in {\mathbb {R}}^{N},\\[5pt] u\in W^{1, p}({\mathbb {R}}^{N}), \end{array} \right . \end{equation*}$$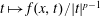 $t\mapsto f(x, t)/|t|^{p-1}$. In particular, both
$t\mapsto f(x, t)/|t|^{p-1}$. In particular, both 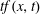 $tf(x, t)$ and
$tf(x, t)$ and 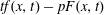 $tf(x, t)-pF(x, t)$ are allowed to be sign-changing in our assumptions.
$tf(x, t)-pF(x, t)$ are allowed to be sign-changing in our assumptions.