Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T07:57:37.283Z Has data issue: false hasContentIssue false
  • English
  • Français

GROEBNER BASES AND NONEMBEDDINGS OF SOME FLAG MANIFOLDS

Part of: Differential topology Computational aspects and applications

Published online by Cambridge University Press:  31 March 2014

ZORAN Z. PETROVIĆ  and
BRANISLAV I. PRVULOVIĆ
ZORAN Z. PETROVIĆ*
Affiliation:
University of Belgrade, Faculty of Mathematics, Studentski trg 16, Belgrade, Serbia email [email protected]
BRANISLAV I. PRVULOVIĆ
Affiliation:
University of Belgrade, Faculty of Mathematics, Studentski trg 16, Belgrade, Serbia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Groebner bases for the ideals determining mod 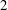$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2$ cohomology of the real flag manifolds 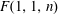$F(1,1,n)$ and 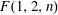$F(1,2,n)$ are obtained. These are used to compute appropriate Stiefel–Whitney classes in order to establish some new nonembedding and nonimmersion results for the manifolds 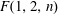$F(1,2,n)$.

Keywords

flag manifoldGroebner basisimmersionembeddingcuplength

MSC classification

Secondary: 13P10: Gröbner bases; other bases for ideals and modules (e.g., Janet and border bases) 57R40: Embeddings 57R42: Immersions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 3 , June 2014 , pp. 338 - 353
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Adams, W. W. and Loustaunau, P., An Introduction to Gröbner Bases, Graduate Studies in Mathematics, 3 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Ajayi, D. O. and Ilori, S. A., ‘Nonembeddings of the real flag manifolds R F (1, 1, n − 2)’, J. Aust. Math. Soc. (Ser. A) 66 (1999), 51–55.CrossRefGoogle Scholar
Becker, T. and Weispfenning, V., Gröbner Bases: A Computational Approach to Commutative Algebra, Graduate Texts in Mathematics (Springer, New York, 1993).CrossRefGoogle Scholar
Borel, A., ‘La cohomologie mod 2 de certains espaces homogènes’, Comm. Math. Helv. 27 (1953), 165–197.Google Scholar
Buchberger, B., ‘A theoretical basis for the reduction of polynomials to canonical forms’, ACM SIGSAM Bull. 10/3 (1976), 19–29.Google Scholar
Hiller, H., ‘On the cohomology of real Grassmannians’, Trans. Amer. Math. Soc. 257 (1980), 521–533.Google Scholar
Korbaš, J. and Lörinc, J., ‘The ℤ2-cohomology cup-length of real flag manifolds’, Fund. Math. 178 (2003), 143–158.Google Scholar
Lam, K. Y., ‘A formula for the tangent bundle of flag manifolds and related manifolds’, Trans. Amer. Math. Soc. 213 (1975), 305–314.CrossRefGoogle Scholar
Milnor, J. W. and Stasheff, J. D., Characteristic Classes, Annals of Mathematics Studies, 76 (Princeton University Press, New Jersey, 1974).CrossRefGoogle Scholar
Petrović, Z. Z. and Prvulović, B. I., ‘On Groebner bases and immersions of Grassmann manifolds G 2, n’, Homology Homotopy Appl. 13(2) (2011), 113–128.CrossRefGoogle Scholar
Sanderson, B. J., ‘Immersions and embeddings of projective spaces’, Proc. Lond. Math. Soc. 14 (1964), 137–153.Google Scholar
Stong, R. E., ‘Cup products in Grassmannians’, Topology Appl. 13 (1982), 103–113.Google Scholar
Stong, R. E., ‘Immersions of real flag manifolds’, Proc. Amer. Math. Soc. 88 (1983), 708–710.CrossRefGoogle Scholar