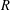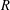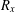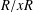Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moradifar, Pooyan
Rajabi, Shahab
and
Yassemi, Siamak
2018.
Tilting modules under special base changes.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 11,
p.
3757.
Zhu, Rongmin
Wei, Jiaqun
and
Di, Zhenxing
2025.
Silting objects under special base changes.
Journal of Algebra,
Vol. 668,
Issue. ,
p.
208.