Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T02:21:27.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating groups for nilpotent varieties

Published online by Cambridge University Press:  09 April 2009

Frank Levin
Frank Levin
Affiliation:
Rutgers, The State University New Brunswick, N.J. 08903U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

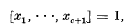Let ℜc denote the variety of all nilpotent groups of class ≦ c, that is, ℜc is the class of all groups satisfying the law, where we define, as usual, 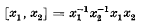and, inductively, 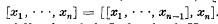. Further, let Fk(ℜc) denote a free group of ℜe of rank k. In her book Hanna Neumann ([4], Problem 14) poses the following problem: Determine d(c), the least k such that Fk(ℜc) generates ℜc. Further, she suggests, incorrectly, that d(c) = [c/2] + l. However, as we shall prove here, the correct answer is d(c) = c—1, for c ≦ 3. 2 More generally, we shall prove the following result.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 1 , February 1970 , pp. 28 - 32
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Kovács, L. G., Newman, M. F. and Pentony, P. F., ‘Generating groups of Nilpotent varieties’, Bull. AMS, 74 (1968), 968–971.CrossRefGoogle Scholar
[2]Baumslag, G., Neumann, B. H., Neumann, Hanna, Neumann, Peter M., ‘On varieties generated by a finitely generated group’, Math. A. 86 (1964), 93–122.Google Scholar
[3]Magnus, W., Karrass, A., Solitar, D., Combinatorial Group Theory (New York and London, Interscience, 1966).Google Scholar
[4]Neumann, Hanna, Varieties of Groups (Berlin, Heidelberg and New York, Springer-Verlag, 1967).CrossRefGoogle Scholar