Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Geluk, J.L.
1996.
Tails of subordinated laws: The regularly varying case.
Stochastic Processes and their Applications,
Vol. 61,
Issue. 1,
p.
147.
Daníelsson, Jón
and
de Vries, Casper G.
1997.
Tail index and quantile estimation with very high frequency data.
Journal of Empirical Finance,
Vol. 4,
Issue. 2-3,
p.
241.
Geluk, J.
de Haan, L.
Resnick, S.
and
Stărică, C.
1997.
Second-order regular variation, convolution and the central limit theorem.
Stochastic Processes and their Applications,
Vol. 69,
Issue. 2,
p.
139.
Drees, Holger
1998.
A general class of estimators of the extreme value index.
Journal of Statistical Planning and Inference,
Vol. 66,
Issue. 1,
p.
95.
Csörgő, Sándor
and
Viharos, László
1998.
Asymptotic Methods in Probability and Statistics.
p.
833.
Peng, L.
1998.
Asymptotically unbiased estimators for the extreme-value index.
Statistics & Probability Letters,
Vol. 38,
Issue. 2,
p.
107.
Drees, Holger
and
Huang, Xin
1998.
Best Attainable Rates of Convergence for Estimators of the Stable Tail Dependence Function.
Journal of Multivariate Analysis,
Vol. 64,
Issue. 1,
p.
25.
de Haan, L.
and
Pereira, T.Themido
1999.
Estimating the index of a stable distribution.
Statistics & Probability Letters,
Vol. 41,
Issue. 1,
p.
39.
Drees, Holger
Resnick, Sidney
and
de Haan, Laurens
2000.
How to make a Hill plot.
The Annals of Statistics,
Vol. 28,
Issue. 1,
Cheng, Shihong
and
Jiang, Changguo
2001.
The Edgeworth expansion for distributions of extreme values.
Science in China Series A: Mathematics,
Vol. 44,
Issue. 4,
p.
427.
Gomes, M.Ivette
and
Martins, M.João
2001.
Generalizations of the Hill estimator – asymptotic versus finite sample behaviour.
Journal of Statistical Planning and Inference,
Vol. 93,
Issue. 1-2,
p.
161.
Alves, M. Isabel Fraga
2001.
Weiss-Hill estimator.
Test,
Vol. 10,
Issue. 1,
p.
203.
Peng, Liang
2001.
Estimating the mean of a heavy tailed distribution.
Statistics & Probability Letters,
Vol. 52,
Issue. 3,
p.
255.
Beirlant, J.
and
Vandewalle, B.
2002.
Some comments on the estimation of a dependence index in bivariate extreme value statistics.
Statistics & Probability Letters,
Vol. 60,
Issue. 3,
p.
265.
SEGERS, JOHAN
2002.
Abelian and Tauberian Theorems on the Bias of the Hill Estimator.
Scandinavian Journal of Statistics,
Vol. 29,
Issue. 3,
p.
461.
Yun, Seokhoon
2002.
On a generalized Pickands estimator of the extreme value index.
Journal of Statistical Planning and Inference,
Vol. 102,
Issue. 2,
p.
389.
Drees, Holger
2002.
Empirical Process Techniques for Dependent Data.
p.
325.
Ferreira, Ana
2002.
Optimal asymptotic estimation of small exceedance probabilities.
Journal of Statistical Planning and Inference,
Vol. 104,
Issue. 1,
p.
83.
Einmahl, John H. J.
and
Lin, Tao
2003.
Asymptotic Normality of Extreme Value Estimators on C[0,1].
SSRN Electronic Journal,
Raoult, J.-P.
and
Worms, R.
2003.
Rate of convergence for the generalized Pareto approximation of the excesses.
Advances in Applied Probability,
Vol. 35,
Issue. 4,
p.
1007.
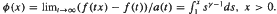 . Then f is said to be of generalized regular variation. In order to control the asymptotic behaviour of certain estimators for distributions in extreme value theory we are led to study regular variation of second order, that is, we assume that
. Then f is said to be of generalized regular variation. In order to control the asymptotic behaviour of certain estimators for distributions in extreme value theory we are led to study regular variation of second order, that is, we assume that 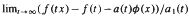 exists non-trivially with a second auxiliary function a1(t). We study the possible limit functions in this limit relation (defining generalized regular variation of second order) and their domains of attraction. Furthermore we give the corresponding relation for the inverse function of a monotone f with the stated property. Finally, we present an Abel-Tauber theorem relating these functions and their Laplace transforms.
exists non-trivially with a second auxiliary function a1(t). We study the possible limit functions in this limit relation (defining generalized regular variation of second order) and their domains of attraction. Furthermore we give the corresponding relation for the inverse function of a monotone f with the stated property. Finally, we present an Abel-Tauber theorem relating these functions and their Laplace transforms.