Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T14:53:55.166Z Has data issue: false hasContentIssue false
  • English
  • Français

The Generalized Inverse A(2)T, S of a Matrix Over an Associative Ring

Part of: Basic linear algebra

Published online by Cambridge University Press:  09 April 2009

Yaoming Yu  and
Guorong Wang
Yaoming Yu
Affiliation:
College of EducationShanghai Normal UniversityShanghai 200234People's Republic of [email protected]
Guorong Wang
Affiliation:
College of MathematicsScience Shanghai Normal UniversityShanghai 200234People's Republic of [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

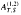In this paper we establish the definition of the generalized inverse A(2)T, S which is a {2} inverse of a matrix A with prescribed image T and kernel s over an associative ring, and give necessary and sufficient conditions for the existence of the generalized inverse and some explicit expressions for 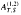of a matrix A over an associative ring, which reduce to the group inverse or {1} inverses. In addition, we show that for an arbitrary matrix A over an associative ring, the Drazin inverse Ad, the group inverse Ag and the Moore-Penrose inverse 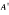. if they exist, are all the generalized inverse A(2)T, S.

MSC classification

Secondary: 15A09: Matrix inversion, generalized inverses
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 83 , Issue 3 , December 2007 , pp. 423 - 438
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Anderson, F. W. and Full, K. R., Rings and Categories of Modules (Springer-Verlag, New York Heidelberg Berlin. 1973).Google Scholar
[2]Ben-Israel, A. and Greville, T. N. E., Generalized Inverses: Theory and Applications. 2nd edition (Springer Verlag, New York, 2003).Google Scholar
[3]Drazin, M. P., ‘Pseudo-inverses in associative rings and semigroups’, Amer. Math. Monthly 65 (1958), 506–514.CrossRefGoogle Scholar
[4]Gouveia, M. C. and Puystjens, R.. –About the group inverse and Moore-Penrose inverse of a product’. Linear Algebra Appl. 150 (1991), 361–369.Google Scholar
[5]Nashed, M. Z. (ed.), Generalized Inverses and Applications (Academic Press, New York. 1976).Google Scholar
[6]Patrício, P., ‘The Moore-Penrose inverse of von Neumann regular matrices over a ring’, Linear Algebra Appl. 332 –334 (2001), 469–483.CrossRefGoogle Scholar
[7]Puystjens, R. and Gouveia, M. C., ‘Drazin invertiblity for matrices over an arbitrary ring’, Linear Algebra Appl. 385 (2004), 105–116.CrossRefGoogle Scholar
[8]Puystjens, R. and Hartwig, R. E., –The group inverse of a companion matrix’, Linear Multilinear Algebra 43 (1997), 137–150.Google Scholar
[9]Bhaskara Rao, K. P. S., The Theory of Generalized Inverses over Commutative Rings, volume 17 of Algebra, logic and Applications Series (Taylor and Francis. London and New York. 2002).CrossRefGoogle Scholar
[10]Wang, G., Wei, Y. and Qiao, S., Generalized Inverses: Theory and Computations (Science Press, Beijing/New York, 2004).Google Scholar
[11]Wei, Y., ‘A characterization and representation of the generalized inverse A(2)T, S and its applications’, Linear Algebra Appl. 280 (1998), 87–96.CrossRefGoogle Scholar
[12]Yu, Y. and Wang, G., ‘The existence of Drazin inverses over integral domains’, j. Shanghai Normal University(NS) 32 (2003), 12–15.Google Scholar
[13]Yu, Y. and Wang, G., ‘The generalized inverse A(2)T, S over commutative rings’, Linear Multilinear Algebra 53 (2005), 293–302.Google Scholar