Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T14:29:04.905Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERALIZED CONTINUED FRACTION EXPANSIONS WITH CONSTANT PARTIAL DENOMINATORS

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  21 December 2018

TOPI TÖRMÄ
TOPI TÖRMÄ*
Affiliation:
Research Unit of Mathematical Sciences, P.O. Box 8000, 90014 University of Oulu, Finland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study generalized continued fraction expansions of the form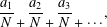

$$\begin{eqnarray}\frac{a_{1}}{N}\frac{}{+}\frac{a_{2}}{N}\frac{}{+}\frac{a_{3}}{N}\frac{}{+}\frac{}{\cdots },\end{eqnarray}$$
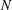where $N$ is a fixed positive integer and the partial numerators 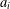$a_{i}$ are positive integers for all 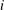$i$. We call these expansions 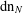$\operatorname{dn}_{N}$ expansions and show that every positive real number has infinitely many 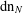$\operatorname{dn}_{N}$ expansions for each 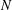$N$. In particular, we study the 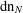$\operatorname{dn}_{N}$ expansions of rational numbers and quadratic irrationals. Finally, we show that every positive real number has, for each 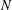$N$, a 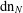$\operatorname{dn}_{N}$ expansion with bounded partial numerators.

Keywords

generalized continued fractions

MSC classification

Primary: 11J70: Continued fractions and generalizations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 2 , October 2019 , pp. 272 - 288
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Anselm, M. and Weintraub, S. H., ‘A generalization of continued fractions’, J. Number Theory 131 (2011), 2442–2460.Google Scholar
Berndt, B. C., Ramanujans Notebooks, Part II (Springer, New York, 1989).Google Scholar
Berndt, B. C., Ramanujans Notebooks, Part III (Springer, New York, 1991).Google Scholar
Borwein, J., Crandall, R. and Fee, G., ‘On the Ramanujan AGM fraction. Part I: the real-parameter case’, Exp. Math. 13 (2004), 275–286.Google Scholar
Borwein, J., van der Poorten, A., Shallit, J. and Zudilin, W., Neverending Fractions: An Introduction to Continued Fractions, Australian Mathematical Society Lecture Series, 23 (Cambridge University Press, Cambridge, 2014).Google Scholar
Dutka, J., ‘Wallis’s product, Brouncker’s continued fraction, and Leibniz’s series’, Arch. History Exact Sci. 26 (1982), 115–126.Google Scholar
Lorentzen, L. and Waadeland, H., Continued Fractions with Applications, Studies in Computational Mathematics, 3 (North-Holland, Amsterdam, 1992).Google Scholar
Rosen, K. H., Elementary Number Theory and its Applications, 3rd edn (Addison-Wesley, Reading, MA, 1992).Google Scholar