No CrossRef data available.
Article contents
Generalization of a theorem of P. D. Finch's on integration of set-functions
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Mbe a σ-field of subsets of a space X. A partition of Xmeans a countable partition Π of Xinto sets belonging to M; the set of partitions is directed by refinement. A. Kolmogoroff in 1930 [1] discussed an integral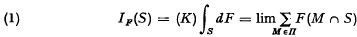 
(Moore-Smith limit as Π gets finer) for set-functions F defined on M. When it exists, IF is σ-additive, and if by chance F is already σ-additive, then IF = F
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1966
References
[1]Kolmogoroff, A., ‘Untersuchung uber das Integralbegriff’, Math. Annalen 103 (1930), 654–698.CrossRefGoogle Scholar
[2]Finch, P. D., ‘Integration of real-valued set functions in abstract spaces’, J. Australian Math. Soc. 4 (1964), 202–213.CrossRefGoogle Scholar
[3]Finch, P. D., ‘A generalization of the Radon-Nikodym theorem’, J. Australian Math. Soc. 5 (1965), 17–24.CrossRefGoogle Scholar
You have
Access