Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T06:10:18.302Z Has data issue: false hasContentIssue false
  • English
  • Français

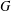THE $G$-CENTRE AND GRADABLE DERIVED EQUIVALENCES

Part of: Modules, bimodules and ideals General and miscellaneous Abelian categories

Published online by Cambridge University Press:  18 June 2018

KEVIN COULEMBIER  and
VOLODYMYR MAZORCHUK
KEVIN COULEMBIER*
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia email [email protected]
VOLODYMYR MAZORCHUK
Affiliation:
Department of Mathematics, University of Uppsala, Box 480, SE-75106, Uppsala, Sweden email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We propose a generalisation for the notion of the centre of an algebra in the setup of algebras graded by an arbitrary abelian group 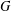$G$. Our generalisation, which we call the 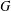$G$-centre, is designed to control the endomorphism category of the grading shift functors. We show that the 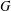$G$-centre is preserved by gradable derived equivalences given by tilting modules. We also discuss links with existing notions in superalgebra theory.

Keywords

group actionsgradingsderived equivalencesgeneralisations of centressuperalgebras

MSC classification

Primary: 16B50: Category-theoretic methods and results (except as in )
Secondary: 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality 18E30: Derived categories, triangulated categories
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 3 , December 2018 , pp. 289 - 315
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

K.C. is supported by Australian Research Council Discover-Project Grant DP140103239. V.M. is supported by the Swedish Research Council and the Göran Gustafssons Foundation.

References

Brundan, J. and Ellis, A. P., ‘Monoidal supercategories’, Comm. Math. Phys. 351 (2017), 1045–1089.Google Scholar
Coulembier, K. and Mazorchuk, V., ‘Dualities and derived equivalences for parabolic category O ’, Israel J. Math. 219(2) (2017), 661–706.Google Scholar
Gorelik, M., ‘On the ghost centre of Lie superalgebras’, Ann. Inst. Fourier (Grenoble) 50(6) (2000), 1745–1764.Google Scholar
Hermann, R., ‘Monoidal categories and the Gerstenhaber bracket in Hochschild cohomology’, Mem. Amer. Math. Soc. 243(1151) (2016), 146 pp.Google Scholar
Rickard, J., ‘Morita theory for derived categories’, J. Lond. Math. Soc. (2) 39(3) (1989), 436–456.Google Scholar
Rickard, J., ‘Derived equivalences as derived functors’, J. Lond. Math. Soc. (2) 43(1) (1991), 37–48.Google Scholar
Rotman, J. J., Advanced Modern Algebra, Graduate Studies in Mathematics, 114 (American Mathematical Society, Providence, RI, 2010).Google Scholar