Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-22T23:06:30.475Z Has data issue: false hasContentIssue false
  • English
  • Français

GAPS IN THE THUE–MORSE WORD

Part of: Elementary number theory Discrete mathematics in relation to computer science Theory of computing

Published online by Cambridge University Press:  25 January 2022

LUKAS SPIEGELHOFER Open the ORCID record for LUKAS SPIEGELHOFER [Opens in a new window]
LUKAS SPIEGELHOFER*
Affiliation:
Mathematics, Montanuniversität Leoben, Leoben, Austria
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Thue–Morse sequence is a prototypical automatic sequence found in diverse areas of mathematics, and in computer science. We study occurrences of factors w within this sequence, or more precisely, the sequence of gaps between consecutive occurrences. This gap sequence is morphic; we prove that it is not automatic as soon as the length of w is at least 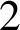$2$ , thereby answering a question by J. Shallit in the affirmative. We give an explicit method to compute the discrepancy of the number of occurrences of the block 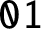$\mathtt {01}$ in the Thue–Morse sequence. We prove that the sequence of discrepancies is the sequence of output sums of a certain base- 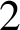$2$ transducer.

Keywords

Thue–Morse sequencesubword occurrencemorphic sequencek-kernel

MSC classification

Primary: 68Q45: Formal languages and automata 68R15: Combinatorics on words
Secondary: 11A63: Radix representation; digital problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 114 , Issue 1 , February 2023 , pp. 110 - 144
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Michael Coons

The author was supported by the Austrian Science Fund (FWF), project F5502-N26, which is a part of the Special Research Program ‘Quasi Monte Carlo methods: Theory and Applications’, and by the FWF-ANR project ArithRand, grant numbers I4945-N and ANR-20-CE91-0006.

References

Allouche, J.-P., Dekking, F. M. and Queffélec, M., ‘Hidden automatic sequences’, Combinatorial Theory 1 (2021): 20.CrossRefGoogle Scholar
Allouche, J.-P. and Shallit, J., ‘The ring of $k$ -regular sequences’, Theoret. Comput. Sci. 98(2) (1992), 163–197.CrossRefGoogle Scholar
Allouche, J.-P. and Shallit, J., ‘The ubiquitous Prouhet–Thue–Morse sequence’, in: Sequences and Their Applications (Proceedings of SETA ‘98, Singapore, 1998), Discrete Mathematics and Theoretical Computer Science (eds. Ding, C., Helleseth, T. and Niederreiter, H.) (Springer, London, 1999), 1–16.Google Scholar
Allouche, J.-P. and Shallit, J., Automatic Sequences: Theory, Applications, Generalizations (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Allouche, J.-P. and Shallit, J., ‘The ring of $k$ -regular sequences. II’, Theoret. Comput. Sci. 307(1) (2003), 3–29.CrossRefGoogle Scholar
Allouche, J.-P. and Shallit, J., ‘Automatic sequences are also non-uniformly morphic’, in Discrete Mathematics and Applications (eds. Raigorodskii, A. M. and Rassias, M. Th.) Springer Optimization and Its Applications, 165 (Springer, Cham, 2020), 1–6.Google Scholar
Berstel, J., ‘Sur la construction de mots sans carré’, in: Séminaire de théorie des nombres (1978–1979) (CNRS, Talence, 1979), Exp. no. 18, 15 pages.Google Scholar
Berstel, J., Axel Thue’s Papers on Repetitions in Words: A Translation, Publications du Laboratoire de Combinatoire et d’Informatique Mathématique, 20 (Université du Québec à Montréal, Montreal, 1995).Google Scholar
Berthé, V. and Bernales, P. C., ‘Balancedness and coboundaries in symbolic systems’, Theoret. Comput. Sci. 777 (2019), 93–110.CrossRefGoogle Scholar
Blanchet-Sadri, F., Currie, J. D., Rampersad, N. and Fox, N., ‘Abelian complexity of fixed point of morphism $\, \, 0\mapsto \mathrm{012,1}\mapsto 02,2\mapsto 1$ ’, Integers 14 (2014), A11, 17 pages.Google Scholar
Brams, S. J. and Taylor, A. D., The Win-Win Solution: Guaranteeing Fair Shares to Everybody (W. W. Norton, New York, 1999).Google Scholar
Brooks, J. L. et al., The Simpsons Movie (20th Century Fox Home Entertainment, Beverly Hills, CA, 2007).Google Scholar
Brown, S., Rampersad, N., Shallit, J. and Vasiga, T., ‘Squares and overlaps in the Thue–Morse sequence and some variants’, RAIRO Theor. Inform. Appl. 40 (2006), 473–484.CrossRefGoogle Scholar
Dekking, F. M., ‘Morphisms, symbolic sequences, and their standard forms’, J. Integer Seq. 19(1) (2016), 16.1.1, 8 pages.Google Scholar
Delange, H., ‘Sur les fonctions $q$ -additives ou $q$ -multiplicatives’, Acta Arith. 21 (1972), 285–298.CrossRefGoogle Scholar
Durand, F., ‘A characterization of substitutive sequences using return words’, Discrete Math. 179(1–3) (1998), 89–101.CrossRefGoogle Scholar
Erdős, P., Mauduit, C. and Sárközy, A., ‘On arithmetic properties of integers with missing digits. I. Distribution in residue classes’, J. Number Theory 70(2) (1998), 99–120.CrossRefGoogle Scholar
Heuberger, C., Kropf, S. and Prodinger, H., ‘Output sum of transducers: limiting distribution and periodic fluctuation’, Electron. J. Combin. 22(2) (2015), 2.19, 53 pages.CrossRefGoogle Scholar
Istrail, S., ‘On irreductible languages and nonrational numbers’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 21(69) (1977), 301–308.Google Scholar
Justin, J. and Vuillon, L., ‘Return words in sturmian and episturmian words’, RAIRO Theor. Inform. Appl. 34(5) (2000), 343–356.CrossRefGoogle Scholar
Lejeune, M., Leroy, J. and Rigo, M., ‘Computing the k-binomial complexity of the Thue–Morse word’, J. Combin. Theory Ser. A 176 (2020), 105284.CrossRefGoogle Scholar
Lothaire, M., Algebraic Combinatorics on Words, Encyclopedia of Mathematics and Its Applications, 90, A collective work by J. Berstel et al. with a preface by J. Berstel and D. Perrin (Cambridge University Press, Cambridge, 2002).CrossRefGoogle Scholar
Mauduit, C., ‘Multiplicative properties of the Thue–Morse sequence’, Period. Math. Hungar. 43(1–2) (2001), 137–153.CrossRefGoogle Scholar
Rao, M., Rigo, M. and Salimov, P., ‘Avoiding 2-binomial squares and cubes’, Theoret. Comput. Sci. 572 (2015), 83–91.CrossRefGoogle Scholar
Rigo, M. and Salimov, P., ‘Another generalization of abelian equivalence: binomial complexity of infinite words’, Theoret. Comput. Sci. 601 (2015), 47–57.CrossRefGoogle Scholar
Sloane, N. J. A. and The OEIS Foundation Inc., The On-Line Encyclopedia of Integer Sequences, 2021.Google Scholar
Thue, A., ‘Über die gegenseitige Lage gleicher Teile gewisser Zeichenreihen’, Norske vid. Selsk. Skr. Mat. Nat. Kl. 1 (1912), 1–67, reprinted in Selected Mathematical Papers of Axel Thue (T. Nagell, editor) (Universitetsforlaget, Oslo, 1977), 413–478.Google Scholar