A continuous real-linear operator A = A0 + i1A1 + i2A2 + i3A3 on a quaternionic Hilbert space is called sesquihermitian if the linear operators Av are Hermitian; this condition is independent of the choice of quaternion basis (i1,i2,i3). The joint spectral distribution of the Av provides a functional calculus for sesquihermitian operators and real-valued C∞-functions on 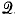. This calculus is independent of the quaternion basis and extends naturally to quaternion-valued functions to give a continuous quaternion-linear mapping from the algebra of these functions to that of sesquihermitian operators. The mapping is not, in general, multiplicative unless the Av commute, in which case it agrees with that for several commuting operators on complex Hilbert space.