Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ahuja, O.P.
1993.
On the generalised Ruscheweyh class of analytic functions of complex order.
Bulletin of the Australian Mathematical Society,
Vol. 47,
Issue. 2,
p.
247.
Li, Jian-Lin
Srivastava, H.M.
and
Zhang, Yu-Lin
1999.
A certain class of analytic functions defined by means of the ruscheweyh derivative.
Complex Variables, Theory and Application: An International Journal,
Vol. 38,
Issue. 1,
p.
85.
Ahuja, Om P.
and
Çetinkaya, Asena
2021.
Mathematical Analysis and Computing.
Vol. 344,
Issue. ,
p.
635.


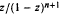 is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.
is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.